15+ Free Converting Repeating Decimals to Fractions Worksheet Pages

These converting repeating decimals to fractions worksheets will help the students to get a proper idea of the repeating decimals and also they will be able to convert them to fractions along with the shortcut method.

---

3 Interactive Ways of Converting Decimals to Fractions

We have differentiated the worksheets into three categories. They are single, multiple, or mixed digits for converting repeating decimals to fractions worksheets. There are 100+ free practice problems in our worksheets.

---

---

Repeating Decimals to Fractions Worksheet: Facts and Examples

Repeating decimals follow a repetitive sequence after the decimal point. The repetitive values can be converted into fractions form. You may be aware of converting fractions to decimals also. Here we have discussed converting repeating decimals to fractions worksheet.

A “terminating decimal” can be converted to a fraction by counting the finite number of digits that follow the decimal point, then multiplying and dividing by the corresponding power of ten.

Example: 0.25= (0.25✕100)/100= 25⁄100=1/4

It is quite simple to convert decimals into fractions. But what about repetitive decimals? The number of decimal places with repeated decimals is limitless, so it is impossible for us to count the repetitive numbers.

Examples of repeating decimals:

0.45454545…….

9.5555555……

15.356356356…..

The above examples show us the repetitive decimals. Let’s jump into the stepwise procedure to convert the repeating decimals to fractions.

---

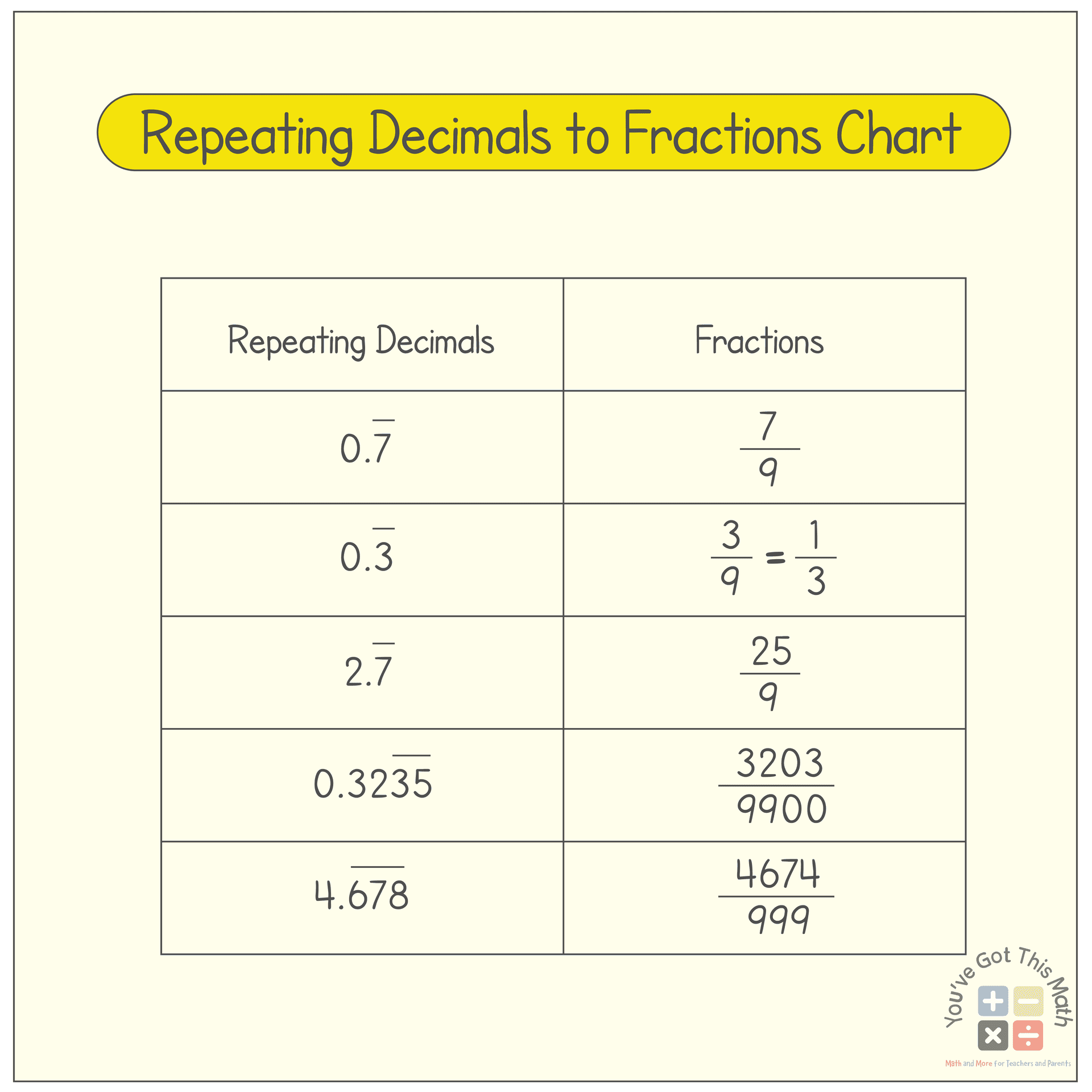
Facts and Charts of Repeating Decimals to Fractions

We have made a chart for different types of repeating decimals to their corresponding fractions form. It will give you a better visualization of the methods. By reading the chart you will get an idea of converting repeating decimals to fractions worksheet.

---

How to Convert Repeating Decimals to Fractions: Learn with Steps!

Suppose, you want to convert 0.55555….to fractions. Follow the below steps to do so.

Step 1: Assume the given decimal number to “x”.

So, we assume x=0.55555….____________(1)

Step 2: Here, the repetitive digit is 5. The number of repetitive digits is 1.

Step 3: After ensuring the repeating digits come after the decimal point, multiply both sides of the equation by a power of ten equal to the number of repeating digits.

We will multiply equation (1) with 10 as we have one repetitive digit.

10x=0.55555….✕10

10x=5.5555……____________(2)

Step 4: At this moment, subtract equation (1) from equation (2).

We will get, 10x-x=5.5555…..- 0.55555…..

From the above equation, we will solve for “x”.

9x=5.

x=5/9.

---

Converting Single Repeating Digit to Fractions

Suppose, you want to convert 0.77777….=0.7 to fractions. Following the below steps you can convert this single repeating digit.

Step 1: Assume the given decimal number to “x”.

So, we assume x=0.77777….____________(1)

Step 2: Here, the repetitive digit is 7. The number of repetitive digits is 1.

Step 3: After ensuring the repeating digits come after the decimal point, multiply both sides of the equation by a power of ten equal to the number of repeating digits. We will multiply equation (1) with 10 as we have one repetitive digit. 10x=0.77777….✕10

10x=7.7777……____________(2)

Step 4: At this moment, subtract equation (1) from equation (2).

We will get, 10x-x=7.7777…..- 0.77777…..

From the above equation, we will solve for “x”.

9x=7.

x=7/9

It is a worksheet PDF of converting repeating decimals to fractions worksheet for single recurring digits.

---

Converting Multiple Repeating Digit to Fractions

Now, we will convert multiple repeating decimals to fractions in these converting decimals to fractions worksheet. Let’s do it. Suppose, we want to convert 4.181818….

Step 1: Assume the given decimal number to “x”.

So, we assume x=4.181818….____________(1)

Step 2: Here, the repetitive digit is 18. The number of repetitive digits is 2.

Step 3: After ensuring the repeating digits come after the decimal point, multiply both sides of the equation by a power of ten equal to the number of repeating digits. Here, the repetitive digit is 2. So, we will multiply both sides with 10²=100. 100x=4.181818….✕100

100x=418.181818……____________(2)

Step 4: At this moment, subtract equation (1) from equation (2). We will get, 100x-x=418.181818………..- 4.181818….

From the above equation, we will solve for “x”.

99x= 414

x=414/99

This is the pdf for converting repeating decimals to fractions worksheet for multiple repeating digits.

---

Mixed Digits Conversion (Repetitive and Non-repetitive)

You may face problems when it comes to solving mixed digits where you have both repetitive and non-repetitive digits. In this converting decimals to fraction worksheet will help the student to understand the mixed digit problems.

Suppose, you want to convert 8.9525252…. To fractions.

Step 1: Assume the given decimal number to “x”. So, we assume x=8.9525252….____________(1)

Step 2: Here, the repetitive digit is 52. The number of repetitive digits is 2 and the only non-repetitive digit is 9.

Step 3: So, we will multiply both sides with 10³=1000 as there are 2 repetitive digits and 1 non-repetitive digit. 1000x=8.9525252….✕1000

1000x=8952.525252……____________(2)

Here, the non-repetitive digit is 3. So, we will multiply both sides with the power of 10.

10x=8.9525252….✕10

10x=89.525252…..____________(3)

Step 4: Now, subtract equation (3) from equation (2).

We will get, 1000x-10x=8952.525252….- 89.525252…..

From the above equation, we will solve for “x”.

990x= 8863

x=8863/990

Here is the pdf file for converting repeating decimals to fractions worksheet of mixed type digits.

---

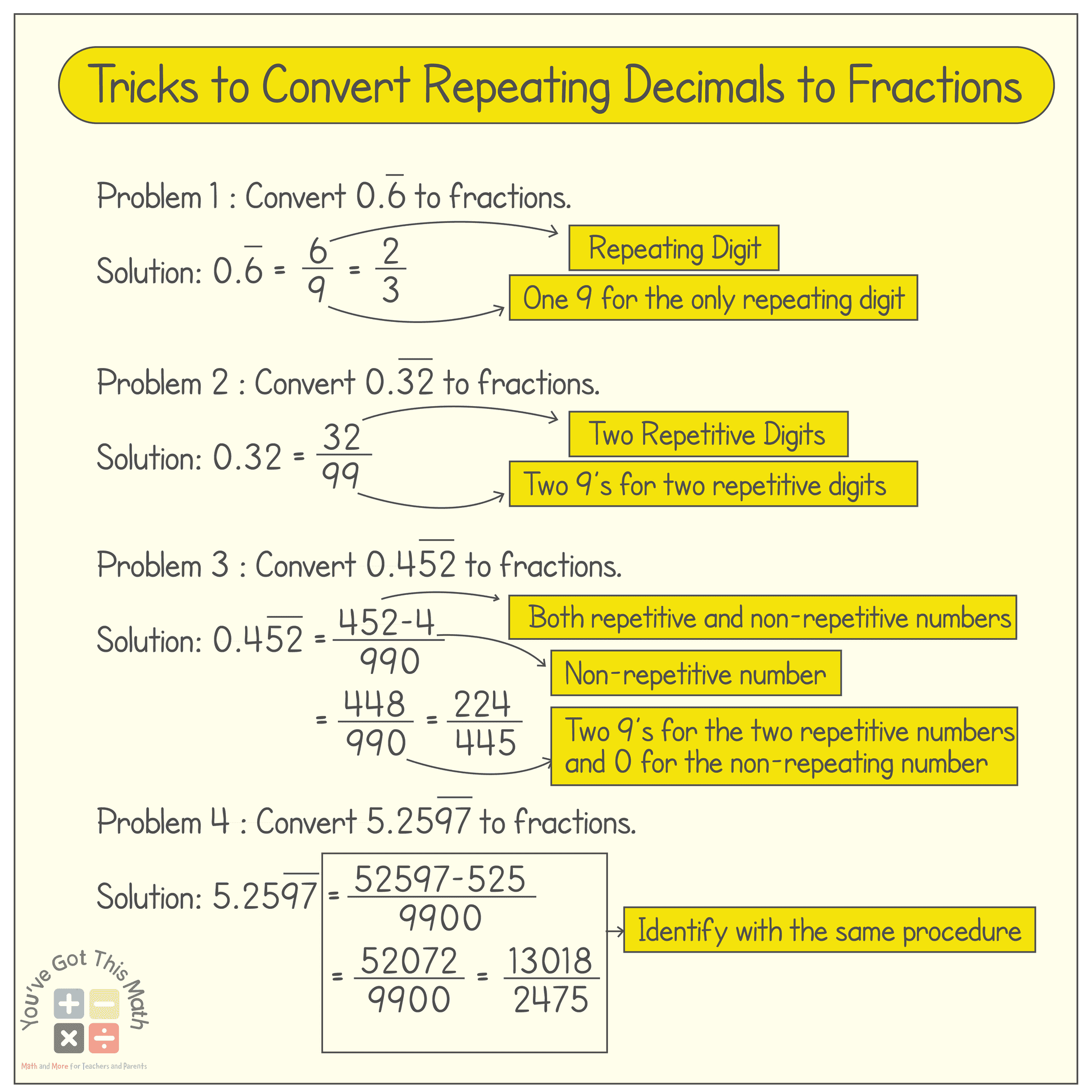
Repeating Decimal to Fraction Conversion: Tips & Tricks

You can convert the decimals to fractions without following the steps described above. Follow the tricks for converting decimals to fractions worksheet.

Decimal type 1: 0.xyz

This trick is suitable only when the repetitive digit is 1. The formula for converting this kind of number is

0.xyz=(Repeated digit or digit)/(Number of 9’s equal to the number of repeated digits)

Example 1: 0.66666…..=0.6 Here, the repetitive digit is 6.

So, the fraction= 6/9

                         = 2/3.

Example 2: 0.323232….=0.32 Here, the repetitive digits are 32.

So, the fraction= 32/99

Decimal type 2: 0. xy…..vw

In the following types, there are some non-repeating digits also.

So, the formula will be 0.xy…..vw=(xyvw-xy)/(Number of 9’s equal to the repetitive digits and Number of 0’s for the non-repetitive terms)

Example 1: 0.4525252…

Here, the repetitive digits are 52 and the non-repetitive digit is 4.

So, the fraction=(452-4)/990

                        =448/990

                         =224/445

Example 2: 5.25979797…

Here, the repetitive digits are 97 and the non-repetitive digits are 525.

So, the fraction=(52597-525)/9900

                          =52072/9900

                          =13018/2475.

---

Download Practice Worksheet PDF

Here is the final worksheet by combining all the worksheets.

---

So, that’s the end of our converting repeating decimals to fractions worksheet. We have discussed 3 different types of repeating decimals and converted them to fractions. Please, download the worksheets and give them to the students for practice.