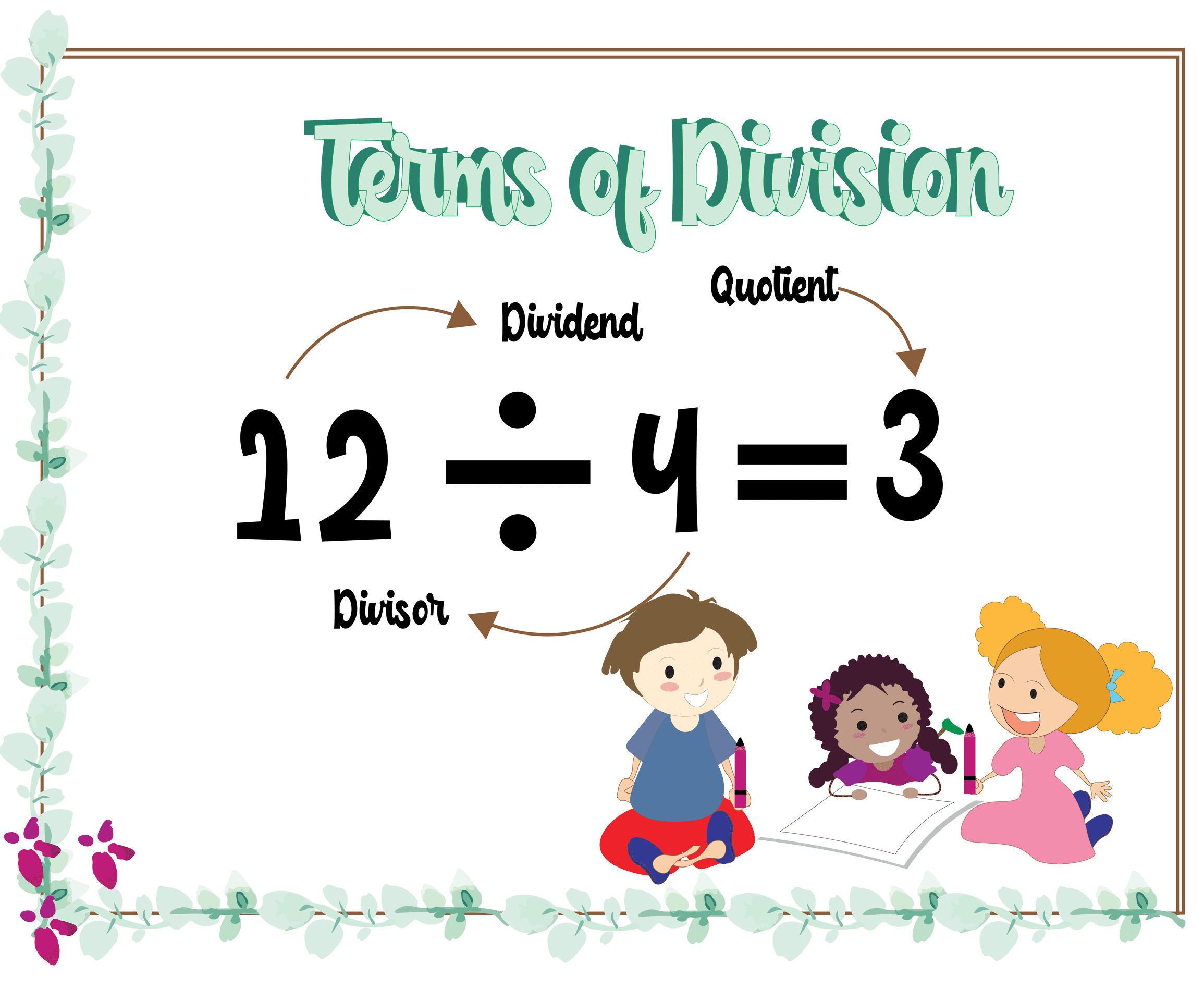6 Probability Worksheet Grade 3 | Free Printable
These probability worksheet grade 3 will help to visualize and understand the probability activities of a student from grade 3. Students will learn basic mathematical operations and can improve their basic math skills with our free printable probability worksheet grade 3.
6 Probability Worksheets for Grade 3
Download the following worksheets and practice with your students to develop the probability activity sense in their juvenile minds.

Probability Worksheets on Candy Jar
Your students need to work with this worksheet carefully. I am taking that your student knows basic probability ideas and can solve the basic problems. Now step into the worksheets. All they need to do is to download the worksheet and read the problems. You can see a candy jar here. The total amount of candies needs to be calculated. Then, answer the questions given in the following of the jar. Solve the problems and have a great time.
Probability Worksheets on School Bag
A picture of a school bag with different stationaries is provided with this worksheet. Count all the stationaries first. Then, answer the questions given in the worksheet.
Probability Worksheets on Color Spinner
You may see a color spinner in your daily life. I have added a color spinner here. Just answer all the questions and have fun with the spinner activity.
Probability Marbles
This activity is quite similar to the first activity. You will get a jar of marbles of different colors. After counting all the marbles, get all the questions answered.
Probability Worksheets on Coin Flip
This activity is quite different. As your students may know, the probability of having a tail or head is ½. Answer all the questions one by one and complete the tasks.
MCQ Test Probability Worksheets
Now, it’s test time. Print the following worksheet, have a pen, and sit down to attend the test. If you can answer all the questions without help, you will be a probability master.
Download the Free PDF
Please download the following combined worksheet and practice with your students.
So today, we’ve discussed probability worksheet grade 3 using activities on candy jar, school bag, color spinner, probability marbles, coin flip, and an MCQ test. Download our free worksheets, and after practicing these worksheets, students will surely improve their mathematical skills and have a better understanding of probability.

Hi there! This is Souptik Roy, a graduate of the Bangladesh University of Engineering and Technology, working as a Content Developer for the You Have Got This Math project of SOFTEKO. I am a person with a curious and creative mind. After finishing my Engineering degree, I want to explore different fields. This is why I am working here as a content developer. I have a massive interest in creative content writing. When I find that someone can learn something from my articles, this gives a lot of inspiration. hopefully, you will find interest in my article, if you have a child and want to teach them math with fun.