60 Fun Area and Perimeter Word Problems | Free Worksheets
These area and perimeter word problems worksheets will help to visualize and understand area and perimeter. 3rd to 5th-grade students will learn the basic techniques to solve area and perimeter related word problems and can improve their basic math skills with our free printable area and perimeter word problems worksheets.
5 Exciting Worksheets for Practicing Area and Perimeter Word Problems
Please download the following word problem worksheets and find area and perimeter on the pages.
Introduction to Area and Perimeter
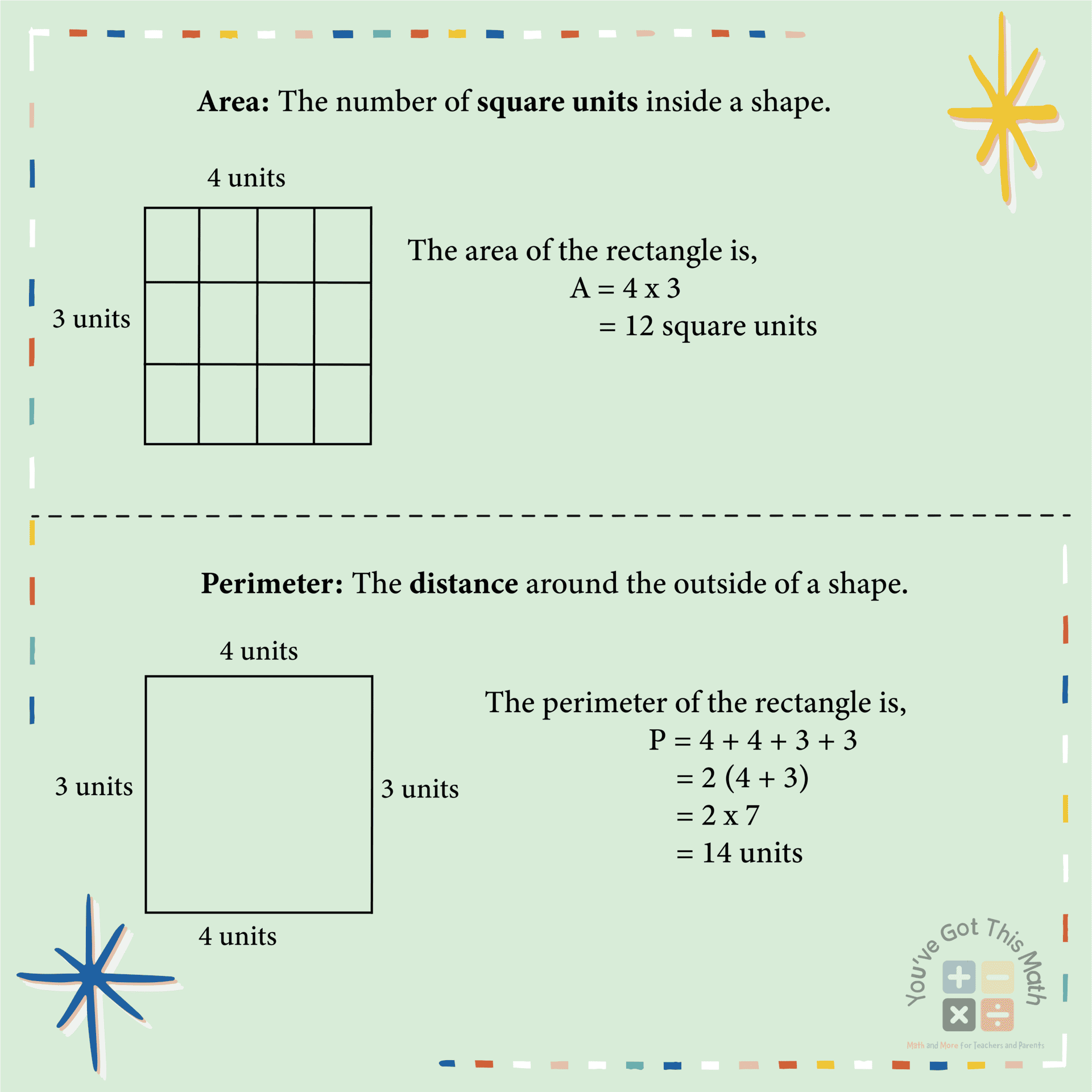
Let’s learn some basics about area and perimeter. In simple words, the area is the whole amount of space inside an object. For example, for the rectangle shown in the following image, the region inside the square shape is its area.
Whereas perimeter is the measured distance around a shape. The following image will give you a better understanding.
It’s a common thing to find the area and perimeter of various shapes. Generally, we calculate these terms for triangular and quadrilateral shapes. But you can also find area and perimeter for other shapes as well.
Triangle Area and Perimeter Word Problems
A space surrounded by three sides is called a triangle. A triangle has three sides and three angles. How can we find the area and perimeter of a triangle?
Follow the below given image below for a better understanding.
If you have understood the above concept, then practice the relevant exercises given in the worksheets.
Quadrilateral Area and Perimeter Word Problems
Quadrilaterals are geometrical shapes that have four sides and four angles. Square, rectangle, parallelogram, rhombus, trapezium, etc. are some of the most known and used quadrilaterals.
The following word problems will help you enhance your skill in finding the area and perimeter of various quadrilaterals.
If you have understood the above concept, then practice the relevant exercises given in the worksheets.
Circle Area and Circumference Word Problems
Another familiar geometrical shape that we see every day is a circle. For a circle, we can also find its area and circumference. We will use the term circumference instead of the perimeter for a circle. Like a perimeter, a circumference is a line that runs around or encircles a circle.
Mainly, it is the outer boundary of a circle. See the following image to get a better understanding of the area and circumference of a circle.
If you have understood the above concept, then practice the relevant exercises given in the worksheets.
Real-Life Area and Perimeter Word Problems
In this section, you will solve some real-life area and perimeter word problems. How are the above shapes related to our real lives, and how can we use tactics to find areas and perimeters for these real-world shapes? We will find out the answers to the above questions in the following worksheets.
Polygon Area and Perimeter Word Problems
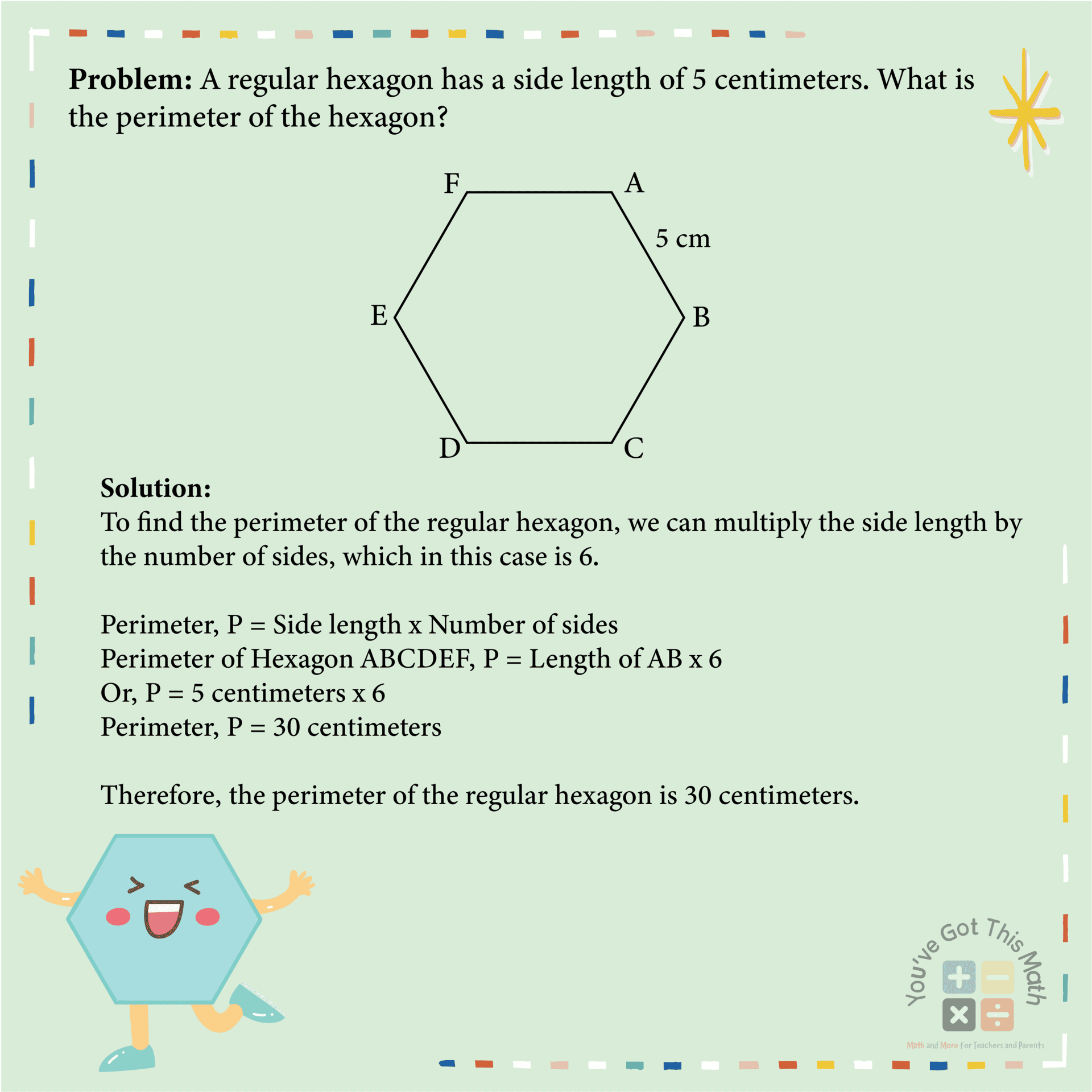
Finally, we are going to solve some perimeter word problems for regular polygons. Here, we will take polygon shapes that have more than four sides. We will find only the perimeters of these shapes.
How we will do that, is explained in the following image.
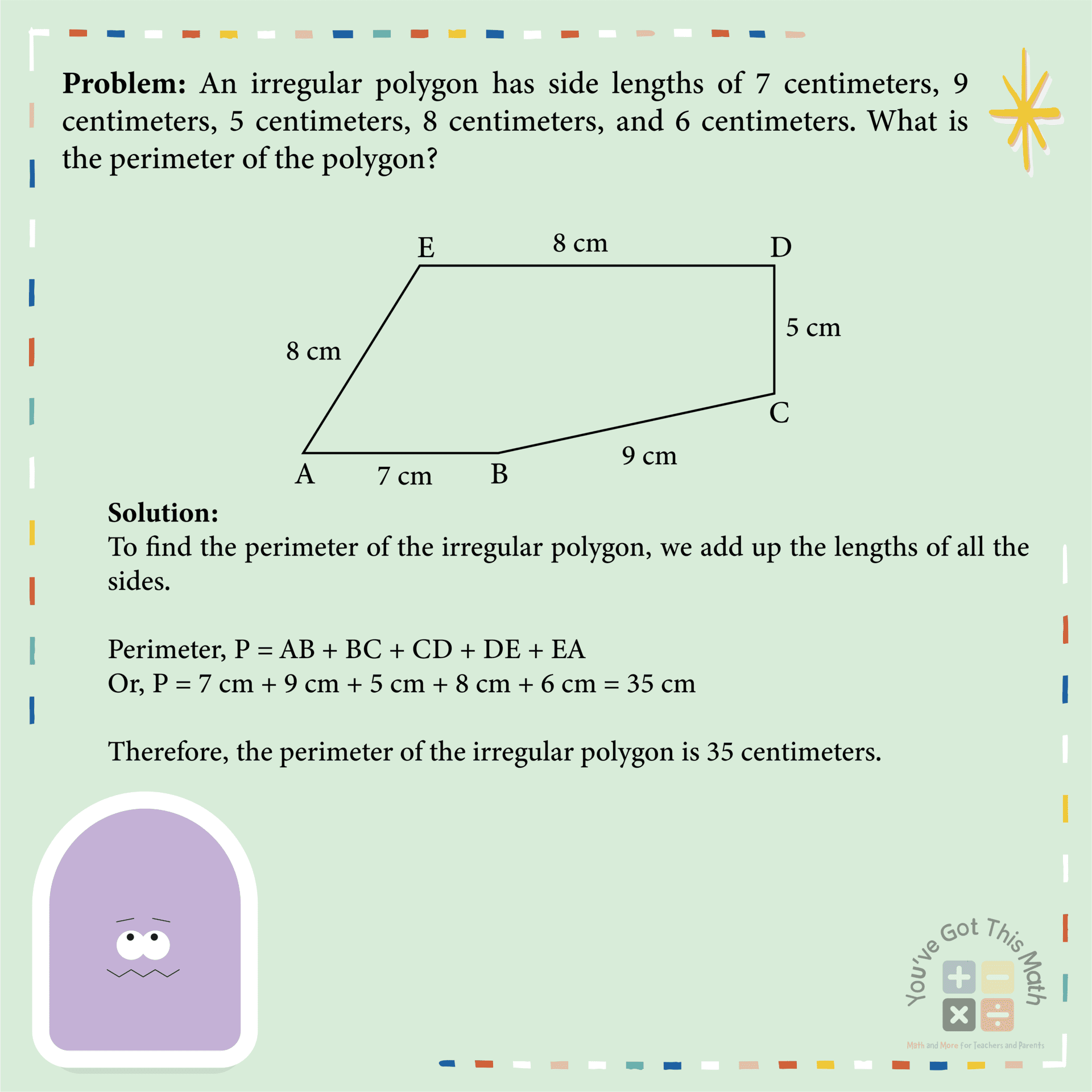
Also, if the polygon is not regularly shaped, then you have to add all the sides of that irregular polygon to get its perimeter. Like we did in the following image.
If you have understood the above concept, then practice the relevant exercises given in the worksheets.
Area and Perimeter Word Problems Challenge
A rectangular floor has dimensions of 10 feet by 12 feet. You want to cover the floor with square tiles that are 1 foot by 1 foot. What is the total number of tiles you need to cover the floor, and what is the perimeter of the tiled floor?
Solution: First, let’s calculate the area of the rectangular floor:
Area of floor = length x width = 10 feet x 12 feet = 120 square feet
Since each tile is 1 foot by 1 foot, the area of one tile is 1 square foot. To find the number of tiles
needed to cover the floor, we can simply divide the area of the floor by the area of one tile:
Number of tiles = area of floor / area of one tile
Number of tiles = 120 square feet / 1 square foot per tile
Number of tiles = 120 tiles
So you’ll need a total of 120 square tiles to cover the entire floor.
Next, let’s calculate the perimeter of the tiled floor. Since the tiles are each 1 foot by 1 foot, the
perimeter of the tiled floor will be the same as the perimeter of the rectangular floor. The
perimeter of a rectangle is found by adding the lengths of all four sides. So:
Perimeter of floor = 2(length + width)
Perimeter of floor = 2(10 feet + 12 feet)
Perimeter of floor = 2(22 feet)
Perimeter of floor = 44 feet
Therefore, the perimeter of the tiled floor is 44 feet.
Download Free Printable Worksheet PDF
Download the following combined PDF and enjoy your practice session.
So today, we’ve discussed area and perimeter word problems worksheets using the concepts of area and perimeter of various geometrical shapes induced with some interactive word problems. Download our free worksheets, and after practicing these worksheets, students will surely improve their mathematical skills and have a better understanding of area and perimeter related word probelms.