Formula for Surface Area of a Triangular Pyramid | 6 Free Worksheets
These worksheets on formula for surface area of a triangular pyramid will help to visualize and understand surface area of a triangular pyramid. 3rd & 4th-grade students will learn basic geometric methods and can improve their basic geometric skills with our free printable worksheets.
6 Worksheets for Formula for Surface Area of a Triangular Pyramid
Download the following worksheets to calculate the surface area of a triangular pyramid which is a three-dimensional shape that resembles a pyramid with a triangular base.
These methods are quite effective. These techniques ought to help your young champion create a strong foundation by teaching them the fundamentals of mathematical operation learning.
Follow the detailed instructions provided below. You can also arrange interactive games using these activities to make learning more effective.
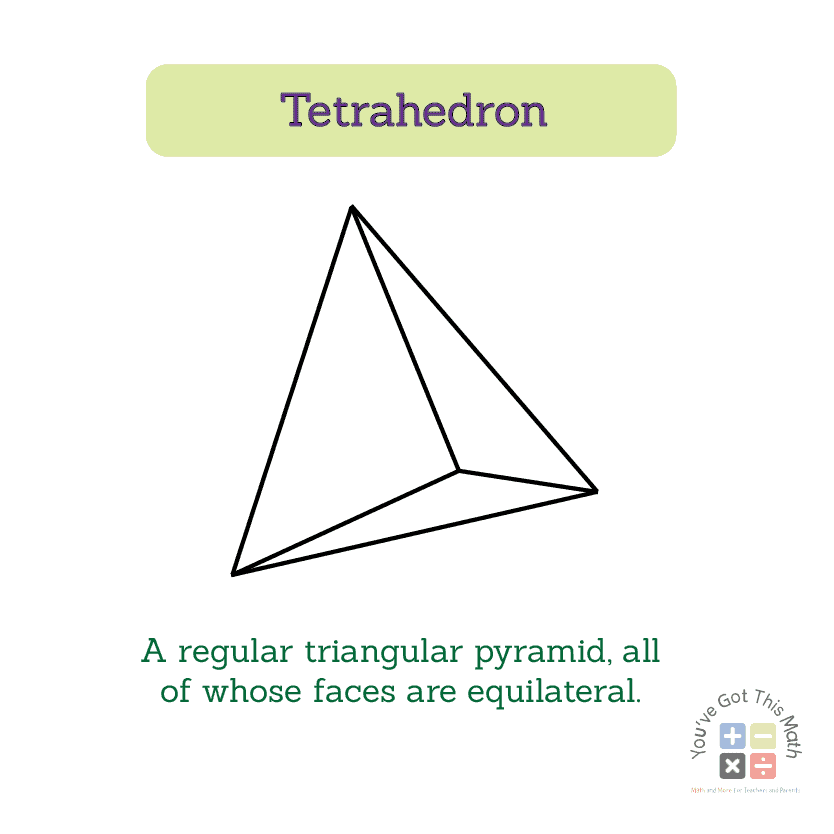
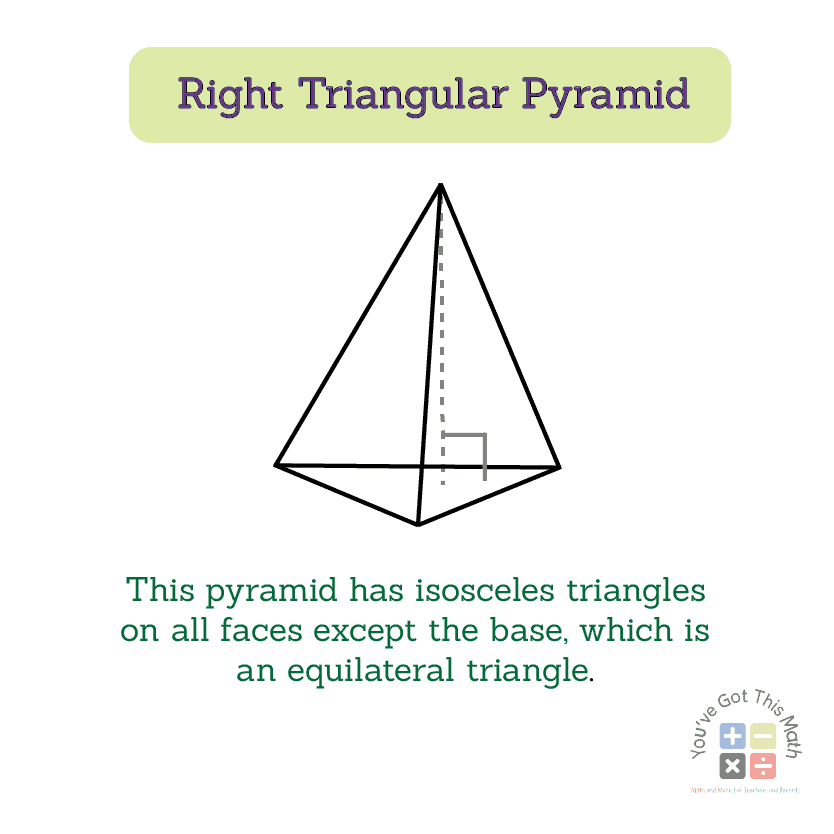
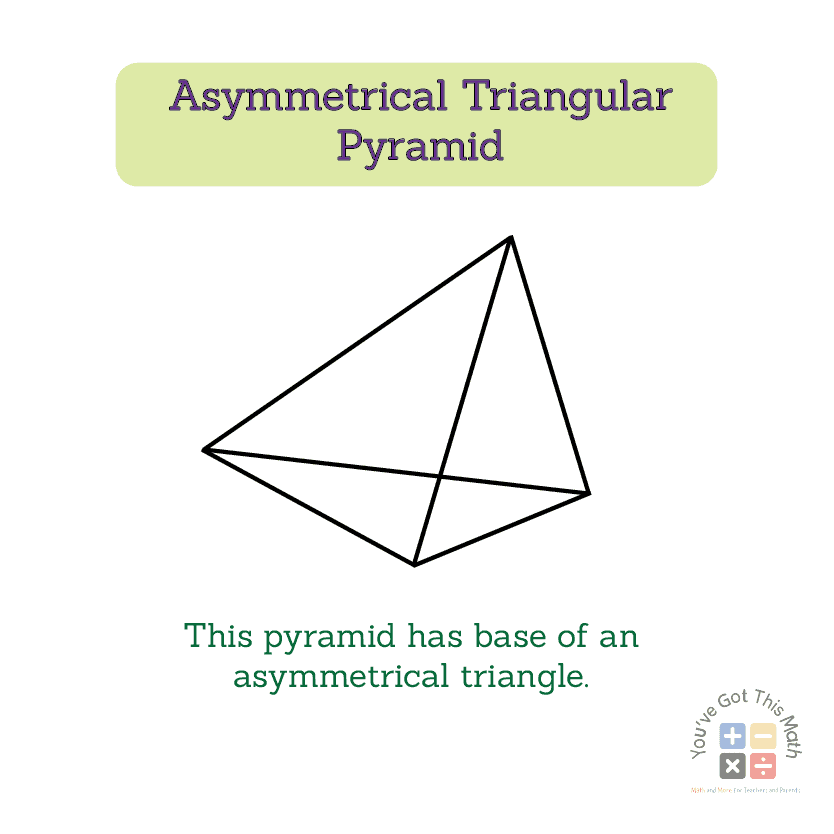
Types of a Triangular Pyramid
- Tetrahedrons are regular triangular pyramids, all of whose faces are equilateral triangles.
- Right triangular pyramid with isosceles triangles on all faces except the base, which is an equilateral triangle.
- A scalene or isosceles triangle serves as the base of an asymmetrical triangular pyramid.
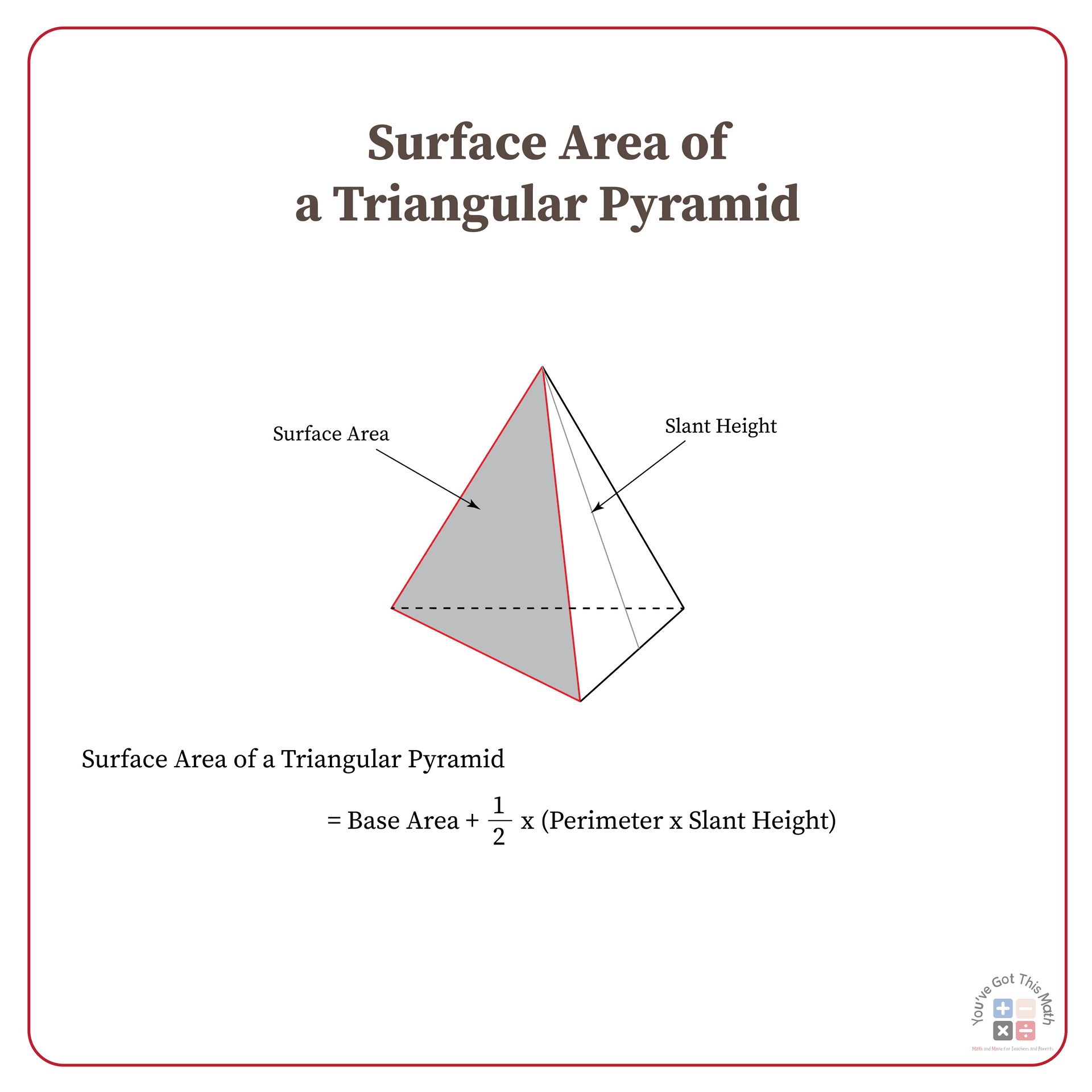
Surface Area of a Triangular Pyramid
Any three-dimensional geometric shape’s surface area equals the sum of all the contained solid’s faces or surfaces. Four triangle-shaped faces make up a triangular pyramid. As a result, the area of the base, its perimeter, and any side’s slant height are all factors in the formula used to determine a triangle pyramid’s surface area. The surface area is always measured in square units like cm^2, m^2, or ft^2.
The surface area of a triangular pyramid is = Base Area + ½ (Perimeter x Slant Height)
2 Effective Formula for Surface Area of a Triangular Pyramid
The lateral surface area and the total surface area are the two different types of surfaces that make up a triangular pyramid. A triangular pyramid’s surface area can be calculated by multiplying its base area (again, a triangle) by the sum of its three lateral areas. Let’s examine both in depth.
Lateral Surface Area Formula of a Triangular Pyramid
The whole surface area of a triangular pyramid, excluding the base, is known as the lateral surface area. It is calculated by adding up the triangular faces’ surface areas. You can use the steps below to calculate a triangular pyramid’s lateral surface area:
- Calculate the area of each triangular face: The area of an equilateral triangle can be found using the formula (side length)^2 x √3 / 4.
- Add up the areas of all the triangular faces.
Moreover, you can also use the following formula to get the lateral surface area of the triangular pyramid.
The lateral surface area of a triangular pyramid = ½ x (Perimeter of the base x Slant height)
If the base is an equilateral triangle, the perimeter will be = 3x one side of the triangle
So the lateral surface area of the triangular pyramid = 3/2 x (Side length x Slant height)
You will get a solved problem in the following picture regarding the formula for the surface area of a triangular pyramid.

Download the following PDF to practice more to become familiar with the formula for the surface area of a triangular pyramid.
Total Surface Area Formula of a Triangular Pyramid
A surface’s total area is referred to as an object’s total surface area. The pyramid’s base area and lateral surface area are added to determine its overall surface area.
The total surface area of a triangular pyramid = Base Area + Lateral Surface Area. Now, the area of a triangle = ½ x (Base x Height).
So, total surface area = ½ x (Side of the Base x Height of the Base) + 3/2 x (Side length x Slant height).
You will get a solved problem in the following picture regarding the formula for the surface area of a triangular pyramid.

Download the following PDF to practice more to be familiar with formula for surface area of a triangular pyramid.
Download the PDF
Download the following combined worksheets and have fun.
So today, we’ve discussed worksheets on formula for surface area of a triangular pyramid using the concepts of calculating lateral surface area and total surface area. Download our free worksheets, and after practicing these worksheets, students will surely improve their mathematical skills and have a better understanding of geometrical concepts.

Hi there! This is Souptik Roy, a graduate of the Bangladesh University of Engineering and Technology, working as a Content Developer for the You Have Got This Math project of SOFTEKO. I am a person with a curious and creative mind. After finishing my Engineering degree, I want to explore different fields. This is why I am working here as a content developer. I have a massive interest in creative content writing. When I find that someone can learn something from my articles, this gives a lot of inspiration. hopefully, you will find interest in my article, if you have a child and want to teach them math with fun.