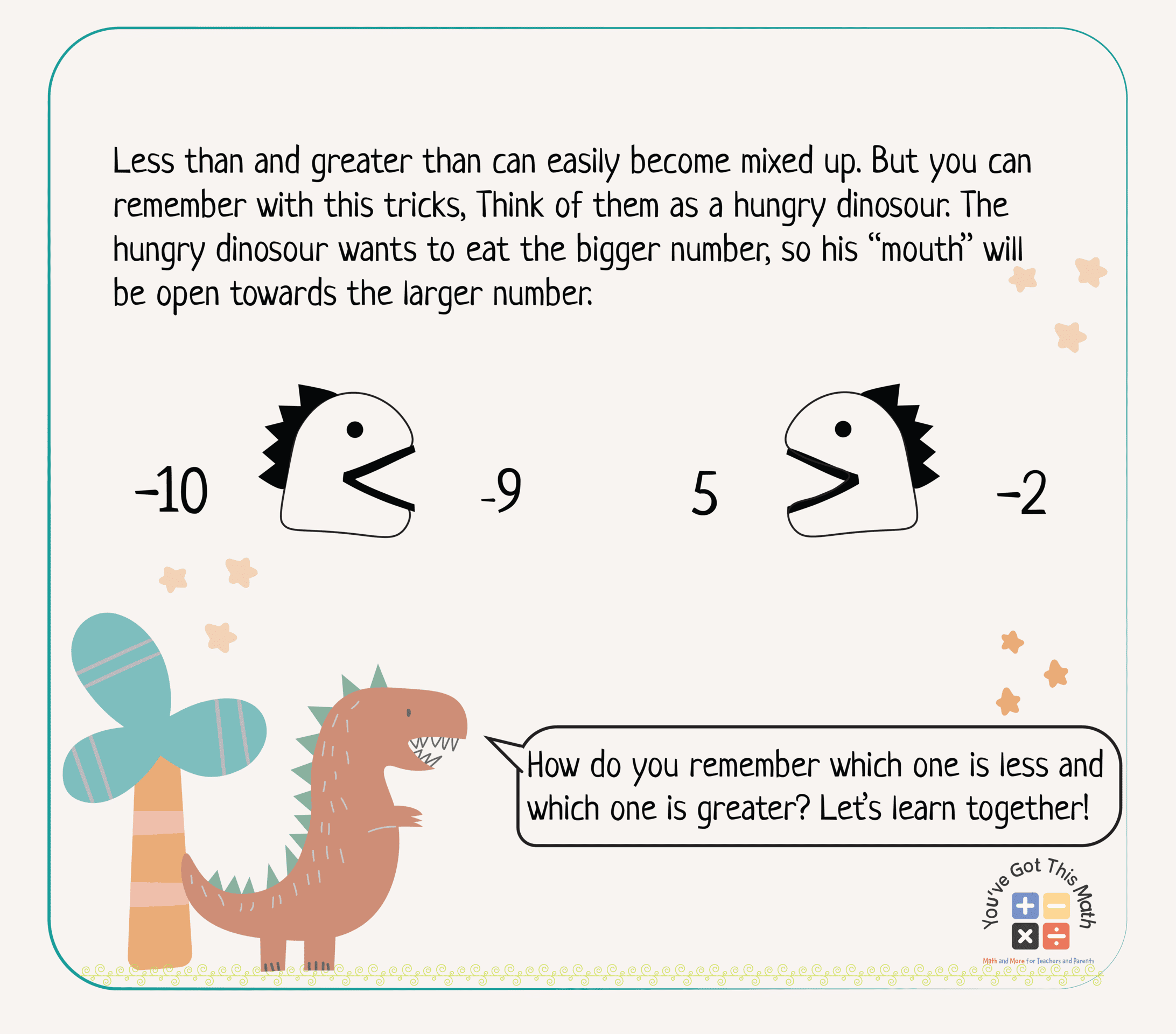7 Free Inequalities on a Number Line Worksheet | Fun Activities
These inequalities on a number line worksheet will help to visualize and understand inequalities on a number line as well as interpret inequalities from a number line. 5th and 6th-grade students will learn the characteristics of inequalities and number lines and can improve their basic math skills with our free printable interactive worksheets.
7 Fun Inequalities on a Number Line Worksheet for Your Youngsters
Please download the following inequalities on a number line worksheet and spot the inequalities on each page.
Definition of Inequalities on a Number Line
Inequalities on a number is a graphical illustration that helps us to visualize values that are represented by an inequality symbol (<,≤,>,≥) or it compares two numbers or expressions, saying which one is greater or less than the other one. When a variable is involved in an inequality, solving an inequality means finding the range of values that the variable can take to make the inequality true.
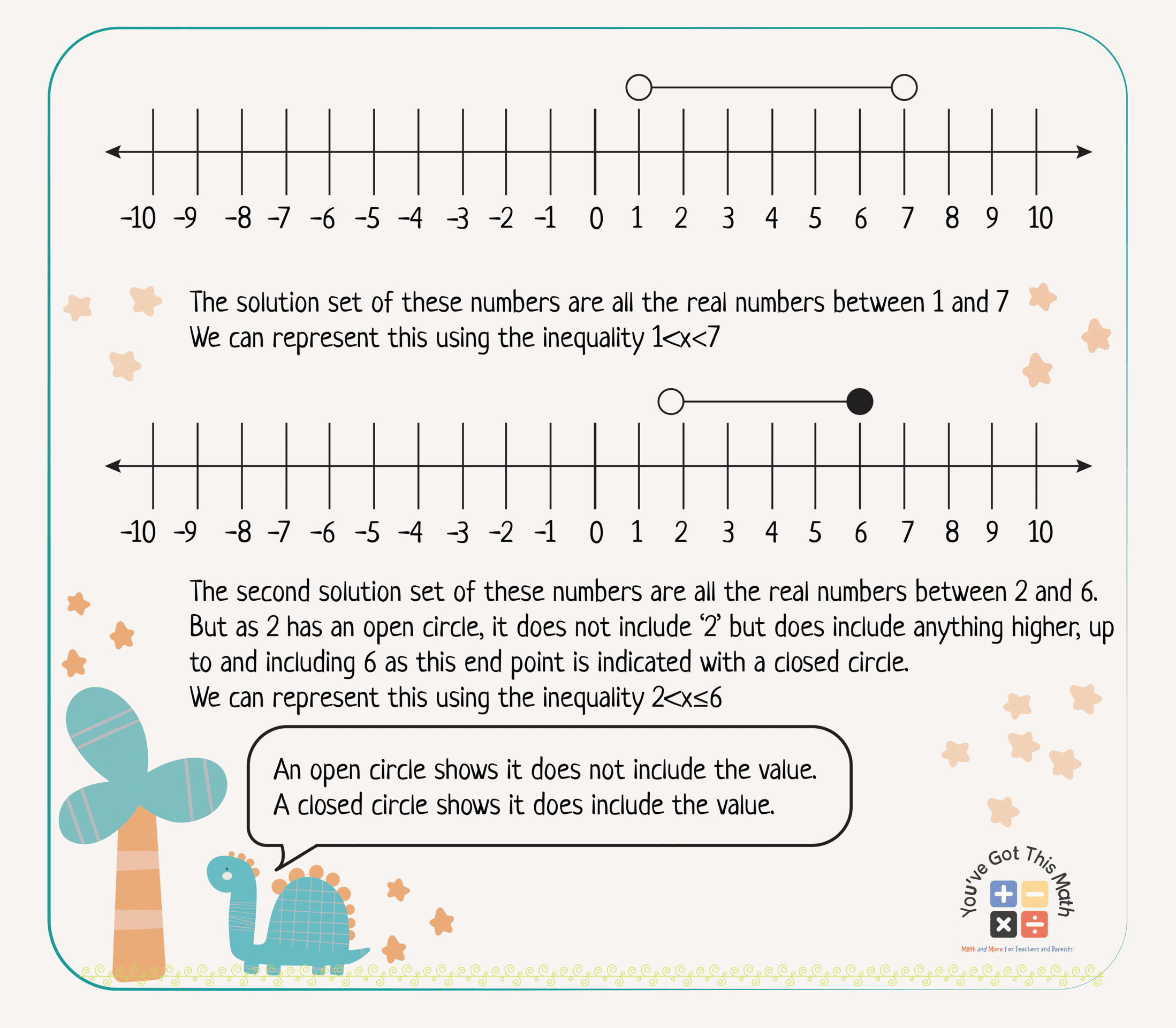
To delineate inequalities on a number line, the range of numbers is shown by drawing a straight line that indicates the endpoints with either an open or closed circle where an open circle means it does not include the value and a closed circle means it does include the value. Let us look at an example to see how. Suppose, “x” is a variant here.
Representing Signs and Graphing Inequalities on a Number Line
In order to represent inequalities on a number, we need to know the basic steps of identification:
⦁ Understand the values so that you can indicate them on the number line.
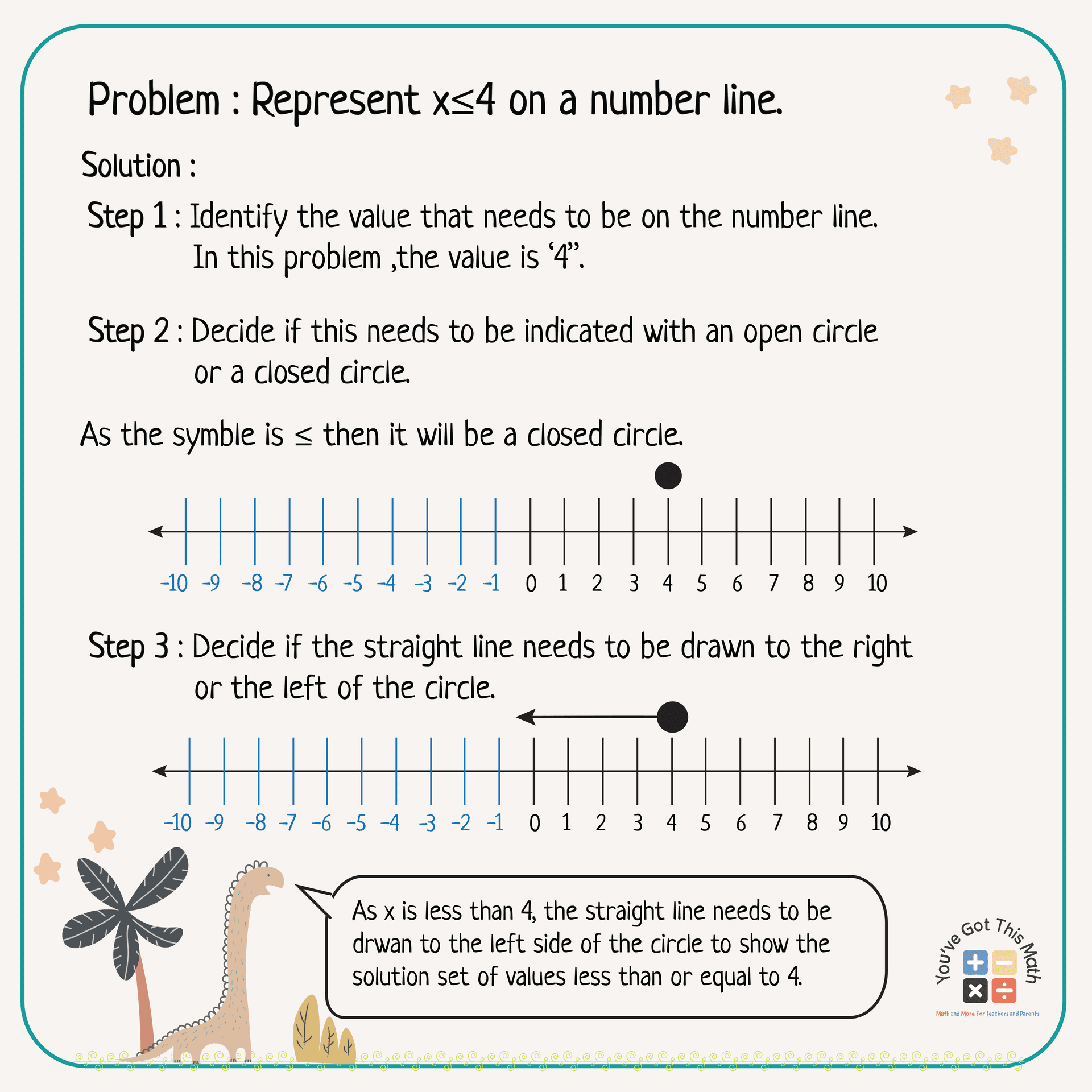
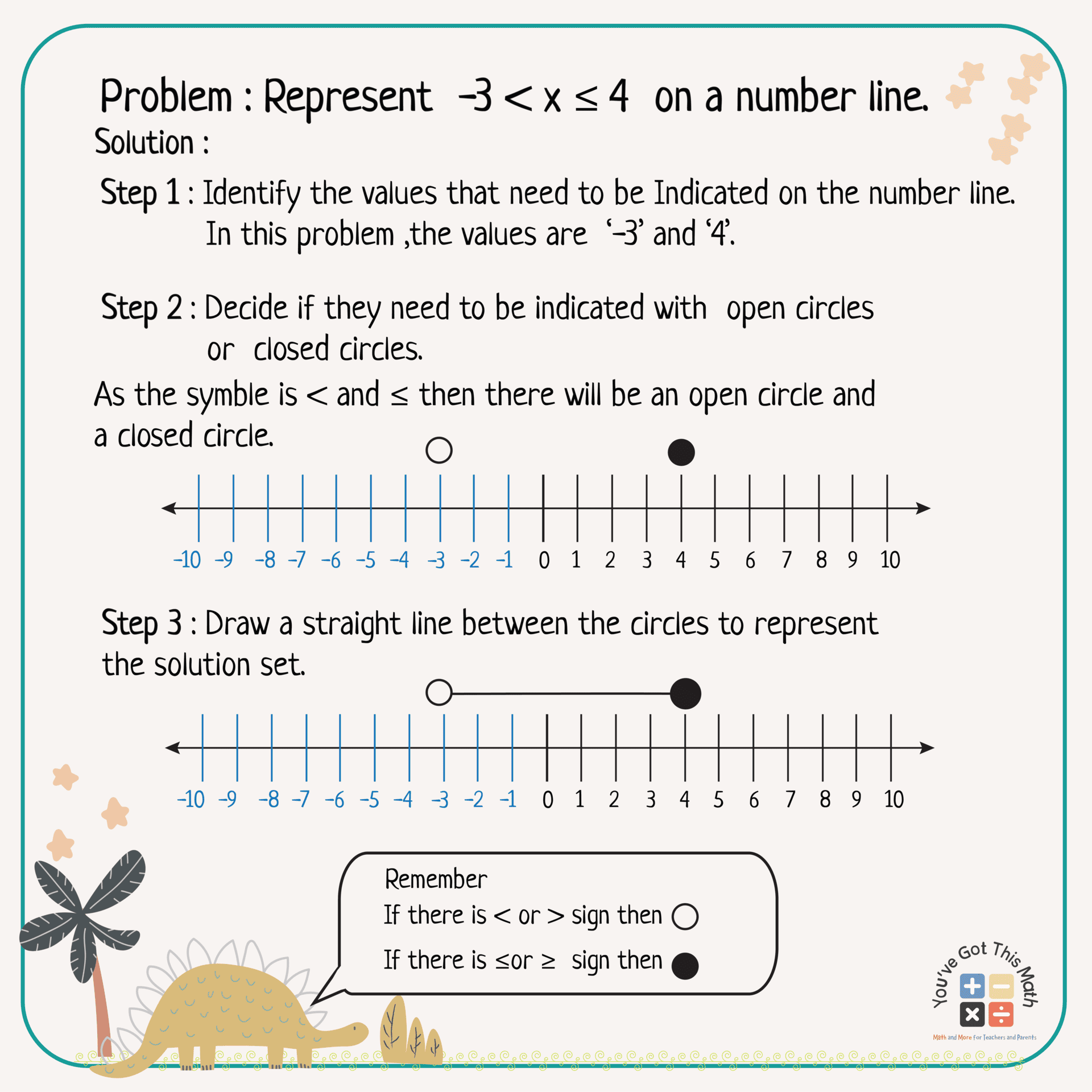
⦁ Now decide if the value needs an open circle or a closed circle
< or > would need an open circle
≤ or ≥ would need a closed circle where
< means less than
> means greater than
≤ means less than or equal to
≥ means greater than or equal to
How do you remember which one is less than and which one is greater than? Let’s learn together with a funny explanation!
⦁ Indicate with a straight line to the left-hand side or right-hand side of the number or with a straight line between the circles.
In the following discussion, we will find some exciting examples and methods of inequalities on a number line.
Illustrate a Line for Inequalities with Single Values
Firstly, we need to identify the values to draw a line for inequalities with a single value. Then after identifying the values you need to decide whether we should use an open circle or a closed circle and draw a straight line to the right or the left of the circle according to the necessity. Let us look at an example. First, we will see what will happen with the sign < or >.
So, now we will learn what will happen with the sign ≤ or ≥.
Test your knowledge afterward with worksheets and exercises.
Inequalities on a Number Line with Values Within a Range
The process is the same as the previous one. At first, we need to identify the values to draw a line for inequalities with the values within a range. Then after identifying the values we need to decide whether we should use an open circle or a closed circle and draw a straight line between the circles according to the solution set. Let’s learn from an example.
Let’s practice with exercises.
Making Equations of Inequalities from Number Line
In the first two methods, we learned how to graph inequalities on a number line. Now, we will do the opposite. We will extract the equation of inequality from a given number line. First, we need to understand the value which is indicated in the number line. Then write the inequality that is shown on this number line using appropriate symbols to express inequalities.
Now test your knowledge afterward with worksheets and exercises.
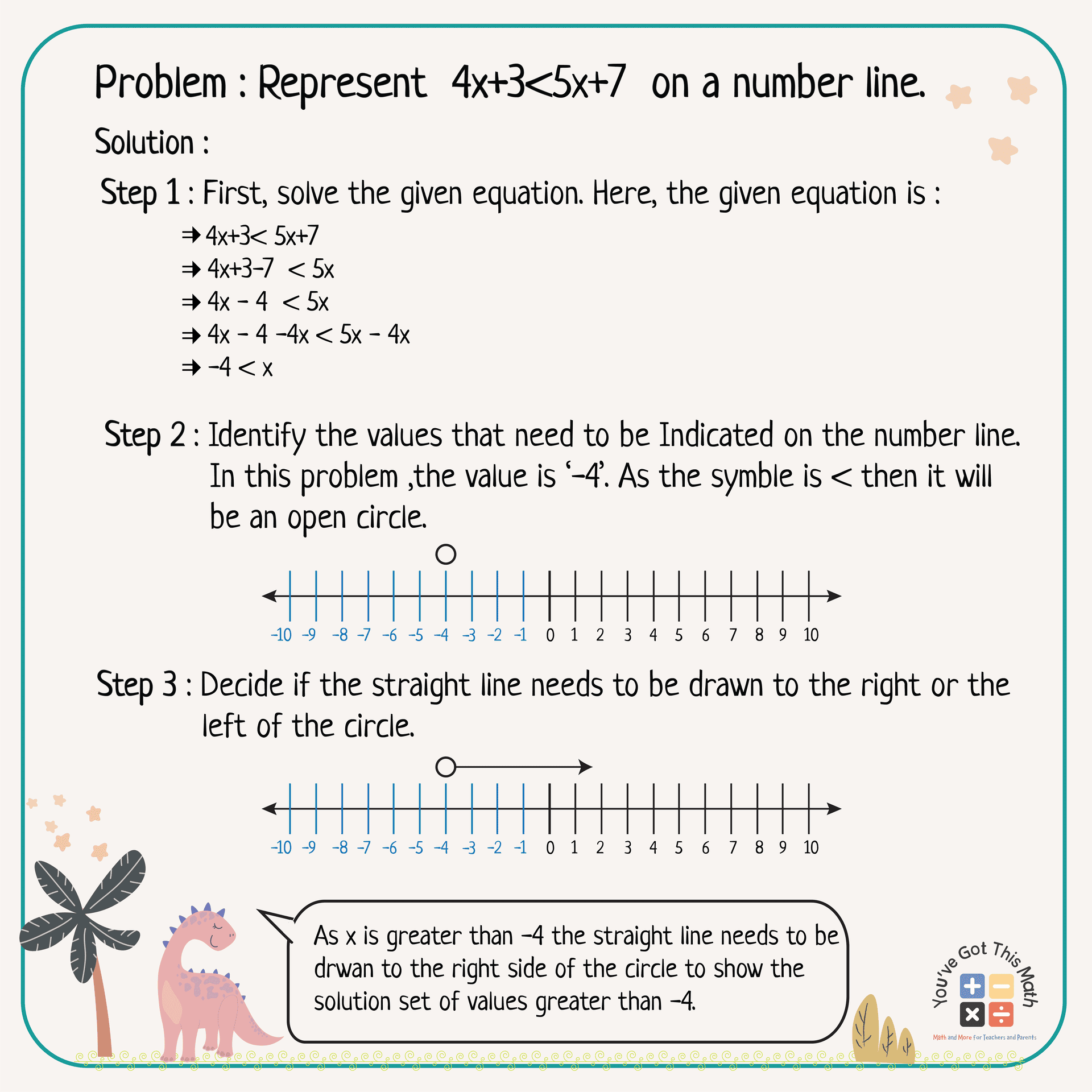
Solve the Equations and Plot Inequalities on a Number Line
We all have learned how to solve a simple equation in our classroom.
This time, we will solve the given equation first. Then we will identify the values from the solution set and draw a line for inequalities. Then after identifying the values we need to decide whether we should use an open circle or a closed circle and draw a straight line between the circles according to the solution set. Let’s learn from an example.
After understanding the above discussion do the following exercises.
Solve These Inequalities and Choose the Right Answer
Here, we will be given an equation of inequalities as well as some options from where we need to choose the right answer for the equation. Firstly we need to identify the values from the given equation and then decide on the correct answer from the given options.
Read each of the inquiries carefully and write the correct answer.
Let’s practice with the given worksheets.
Identify the Correct Inequality on Number Line
Now, we will be given an equation of inequalities as well as some options of graphs from which we need to choose the right answer for the equation. Firstly we need to identify the values from the given equation and then decide on the correct answer from the given options.
Let’s test your knowledge afterward with worksheets and exercises.
Word Problems for Inequalities on a Number Line
Now we will see how to turn a word problem into an inequality. First, solve the inequality by performing the order of operations. Let’s learn with an example.
Practice some word problems to test your knowledge afterward.
Download Free Printable Worksheet PDF
Download the following combined PDF and enjoy your practice session.
So today, we’ve discussed inequalities on a number line worksheet using the concepts of single value inequality, values within a range, making equations, choosing correct answers, plotting graphs, and some interactive word problems. Download our free worksheets, and after practicing these worksheets, students will surely improve their mathematical skills and have a better understanding of inequalities and number line.

Hello! I’m Shamma Tabassum, a Content Developer and Graphic Designer currently working at Softeko. I hold a degree in Architecture from RUET. Throughout my academic journey, I’ve come to view design as a collaborative process rather than something that materializes out of thin air.
Over time, I’ve honed my ability to effectively communicate specific ideas to viewers through my designs and graphical illustrations. I’m always eager to exceed expectations and find innovative ways to present mathematical solutions through out-of-the-ordinary presentations and design.