How to Identify Rational and Irrational Numbers | Free Worksheets
In this article, we will discuss rational and irrational numbers, and do different exercises as well as fun activities to learn more about such numbers. We have given 3 worksheets of rational and irrational numbers. In our Previous article, we discussed prime and composite numbers.
3 Practice Worksheet to Identify Rational and Irrational Numbers
Here, we have given 3 different types of worksheets to identify rational and irrational numbers.
Introduction to Rational and Irrational Numbers
To identify rational and irrational numbers, we have to know about their definitions and differences first. The definitions followed by examples are as follows:
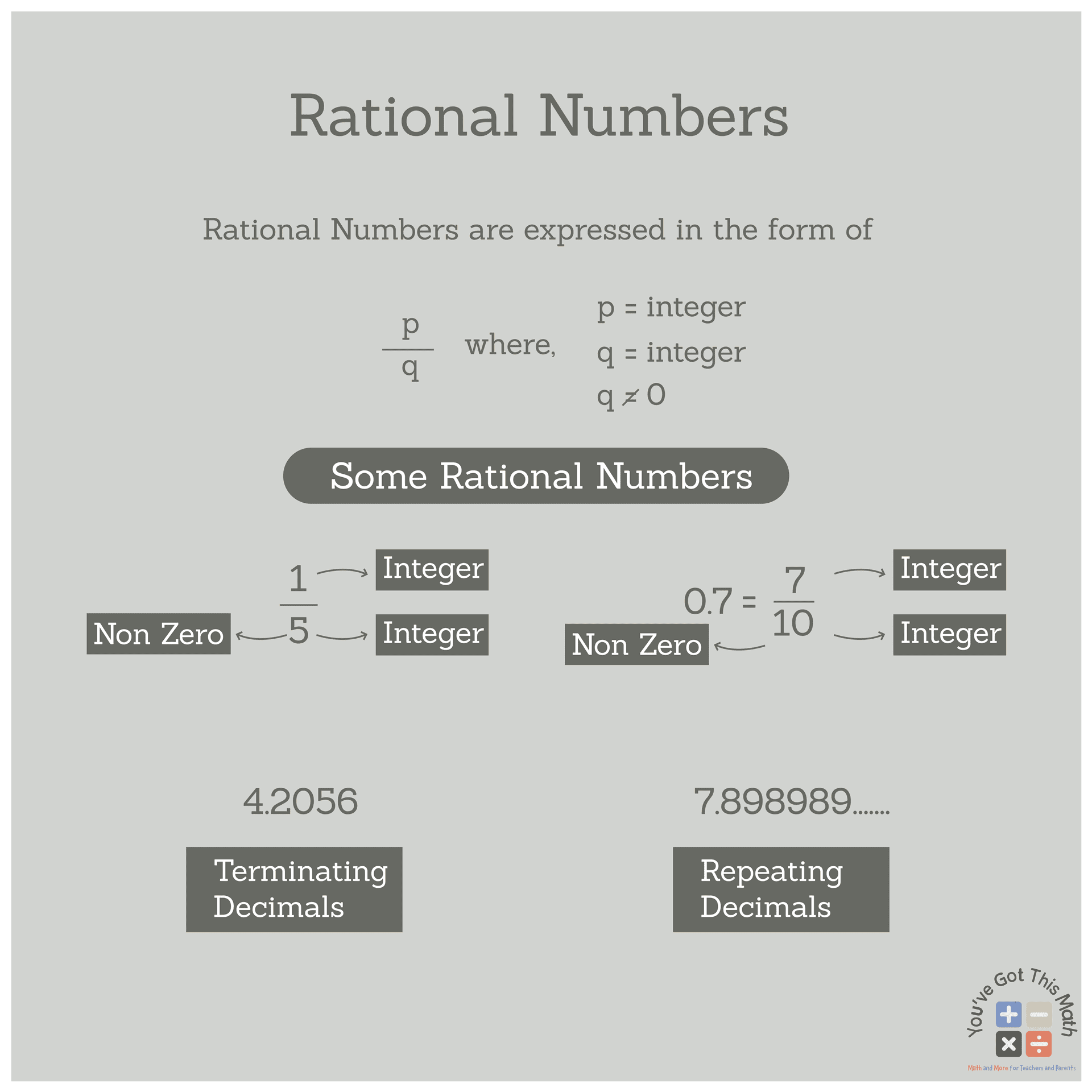
Rational Numbers: The numbers that we can express as the ratio of two integers where the denominator of the fraction is not equal to zero. Rational numbers can be expressed as positive numbers, negative numbers, and zero as well. Integers, fractions (with both numerator and denominator as integers and decimal numbers that have a stopping value and repeating values fall into the category of rational numbers.
Rational Numbers can be expressed as P/Q. Where P and Q are integers and Q is not equal to 0. For instance, ⅕ is a rational number where P=1, Q=5, and Q is not equal to 0. Other examples of rational numbers include 5, 0.7, 4.2056, 7.898989…and so on. This is explained as follows:
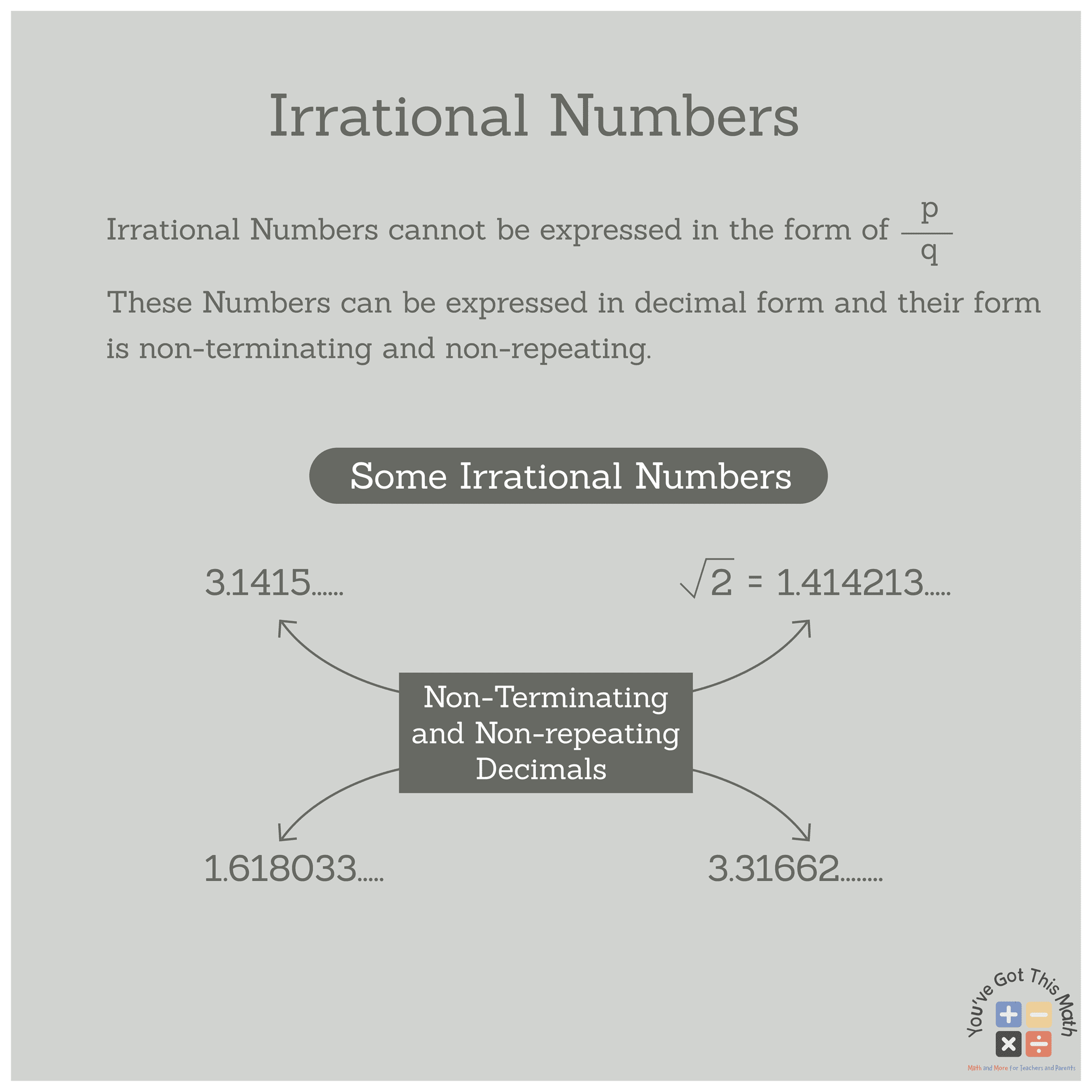
Irrational Numbers: The numbers that we cannot express as the ratio of two integers are known as irrational numbers. We cannot write these numbers in fractions but we can do so in terms of decimals. Their decimal forms do not stop and do not repeat. For example, 3.1415….., √2, 1.618033……., 3.31662……where all these numbers cannot be expressed as P/Q and the decimal values do not stop and do not repeat.
Difference Between Rational and Irrational Numbers
There are some key differentiating points between rational and irrational numbers. We have briefly listed them as follows:
- Rational Numbers can be expressed as a ratio of two integers whereas Irrational Numbers can never be expressed as a ratio of two integers.
2. The perfect square numbers are rational numbers but surds are irrational numbers. Surds are the square roots of numbers that have decimal values that go on without repeating.
3. The decimal value for rational numbers is finite or recurring but for the irrational numbers, it is non-recurring and non-terminating.
Identifying Rational and Irrational Numbers
Let us try to identify whether a number is rational or irrational by going through the following steps mentioned followed by some examples.
Step 1: In the beginning, we check whether a number is an integer or a fraction. If the number is an integer, it is a rational number. If the number is a fraction where both the numerator and the denominator is an integer, then the number is a rational number.
If none of the above cases is true, we need to jump into the next step to find the nature of the number. For instance, if the number is 2, 3, -6 or any other integer, it is a rational number. If the number is ⅗, where 3 and 5 both are integers, the fraction ⅗ is also a rational number.
Step 2: We write the number in its decimal form. If the decimal place values end at some point, then the number will be rational. If that is not the case, then we move on to step 3. For example, if the number is 2.5632354 where the decimal values end at some point, then the number 2.5632354 is a rational number.
Step 3: When the number is written in its decimal form and the decimal value has a pattern that repeats, then the number is a rational number. If none of the above criteria are met, then the number is an irrational number. Such as, when the decimal number is 6.125125125… where there is a repeating pattern, the number is a rational number.
Step 4: The square root of a perfect square number is a rational number. On the other hand, the square root of other numbers are irrational.
Identifying Rational and Irrational Numbers with Example Problems
In this segment, we will use the previous steps mentioned and do some example problems to identify rational and irrational problems.
Example Problem 1: Determine whether the numbers are rational or irrational. 7, 0.5, -2.5, √3 , 0.2222…, 0.52525252…, 100/33 , 3.7575… We identify the nature of these numbers similar to the following image:
Example Problem 2: Determine whether the numbers are rational or irrational. 1.73205…., √15 , 22/7, 0.69333…, -0.00008, 23/33, 7.89, -0.232323…. We solve this example problem like the image below:
Example Problem 3: Determine whether the numbers are rational or irrational. √11, √16, 0.29, 6.45333.., 1/9, 0.0001, 65, 4.5236…. Let us look at the following image for the solution:
Properties of Rational and Irrational Numbers
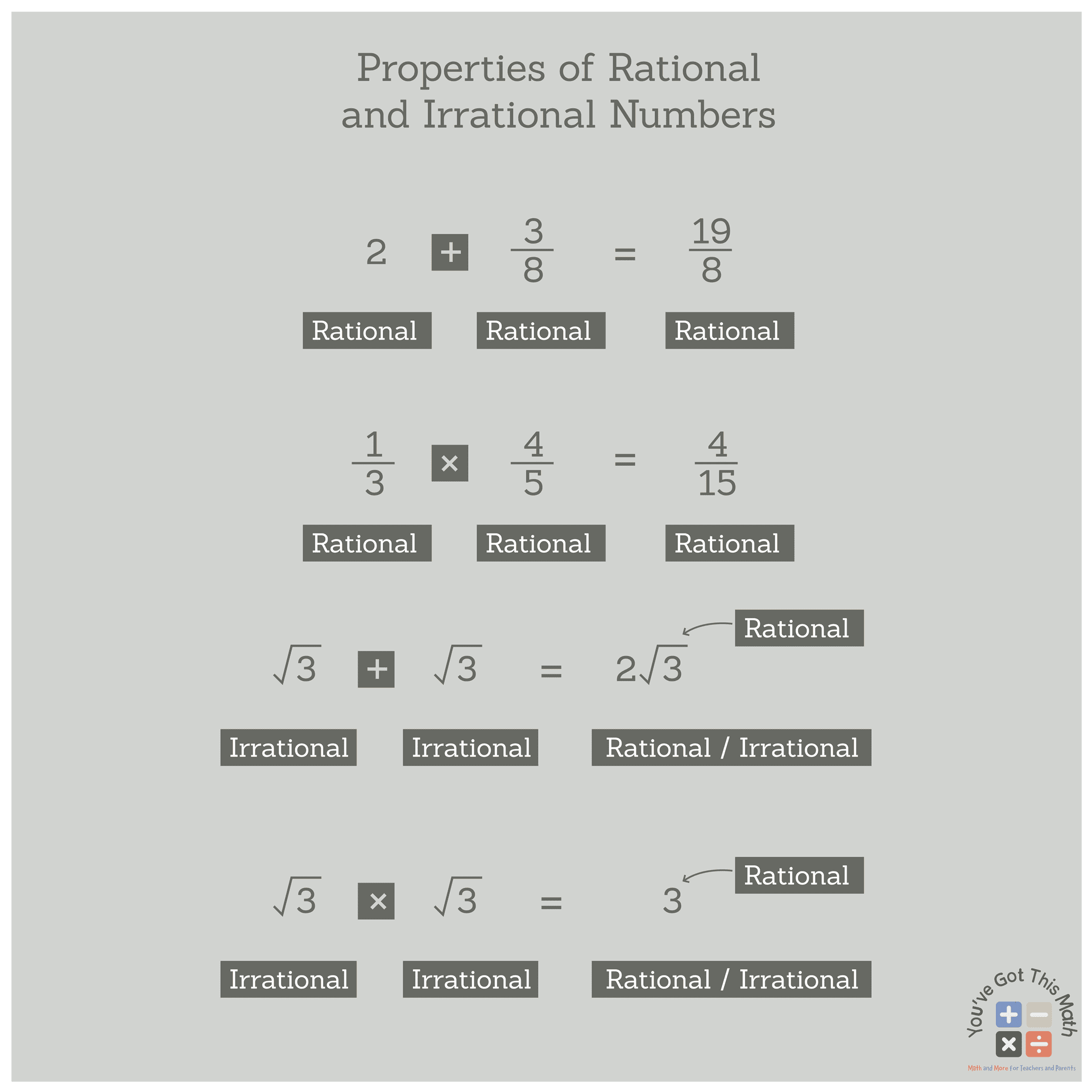
- The sum of two rational numbers is also a rational number. For example, 2+⅜ =19/8 where 2, ⅜ and 19/8 all are rational numbers.
- The product of two or more rational numbers is also a rational number. For example, ⅓ x ⅘ = 4/15; where ⅓, ⅘ and 4/15 are all rational numbers.
- The sum of two irrational numbers is not always irrational. It can be rational as well. For example, √3 + √3 = 2√3 where √3 is an irrational number but its sum with itself gives 2√3 which is a rational number.
- The product of two irrational numbers is not always irrational. It can be rational sometimes. For instance, √3 x √3 = 3 where, √3 is an irrational number but its product with itself is a rational number.
We briefly illustrate these properties in the following image:
3 Fun Activities to Identify Rational and Irrational Numbers
We have done enough discussions and exercises regarding rational and irrational numbers. How does playing some games related to these numbers sound? We will be doing that right away. In this section, we will be doing 3 fun activities to identify rational and irrational numbers. So, without further ado, let’s get into it!
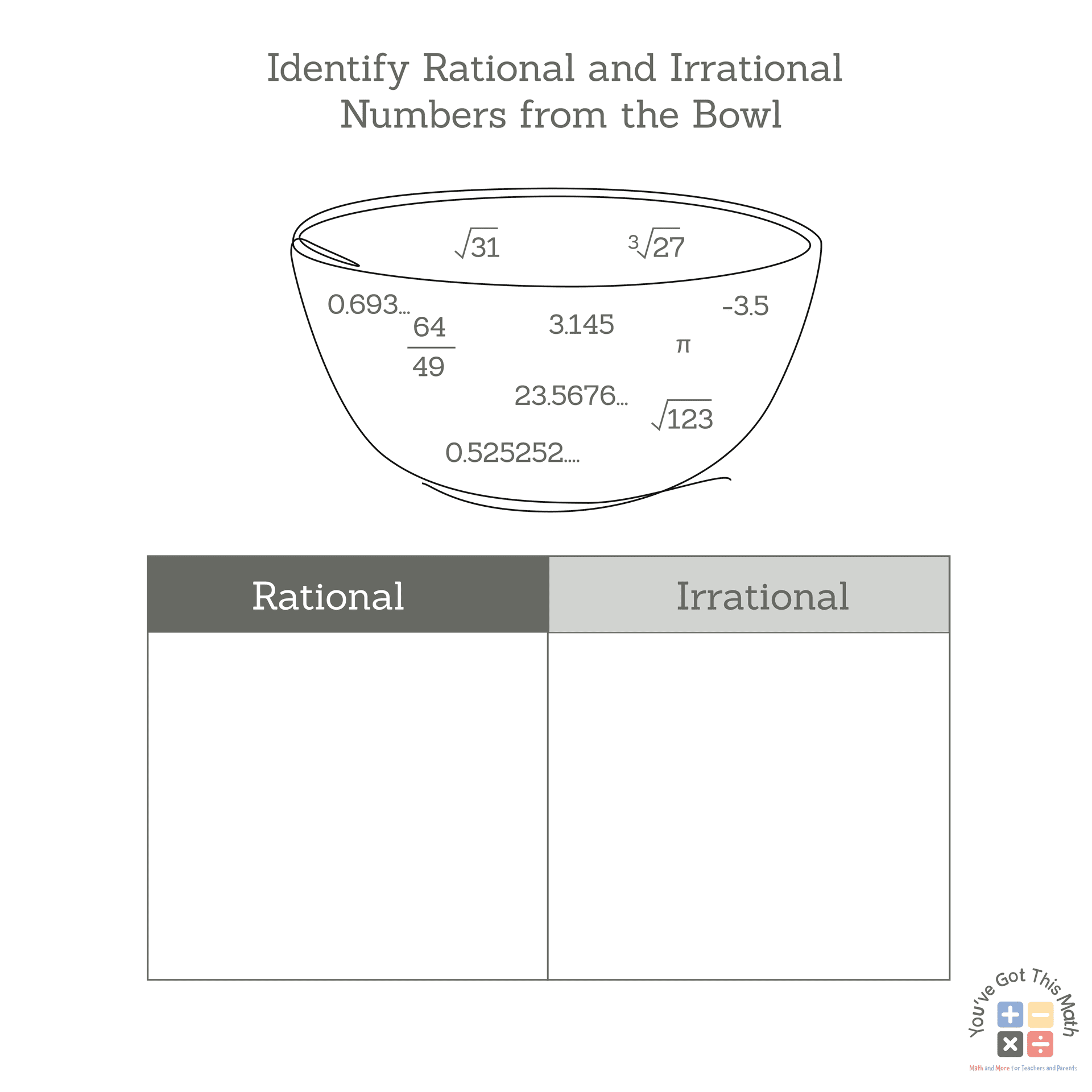
Identify Rational and Irrational Numbers from a Bowl of Numbers
In this activity, we have a list of numbers that are present in some cards within a bowl. With the help of this activity, we will be able to identify rational and irrational numbers by listing and separating the cards that have rational numbers written on them from the ones that have irrational numbers on them.
We pick a card from the bowl and if it contains a rational number, we put it on the Rational Numbers Column. If the number contained is an irrational number, we put it in the Irrational Numbers column. In this way, we list the number of cards.
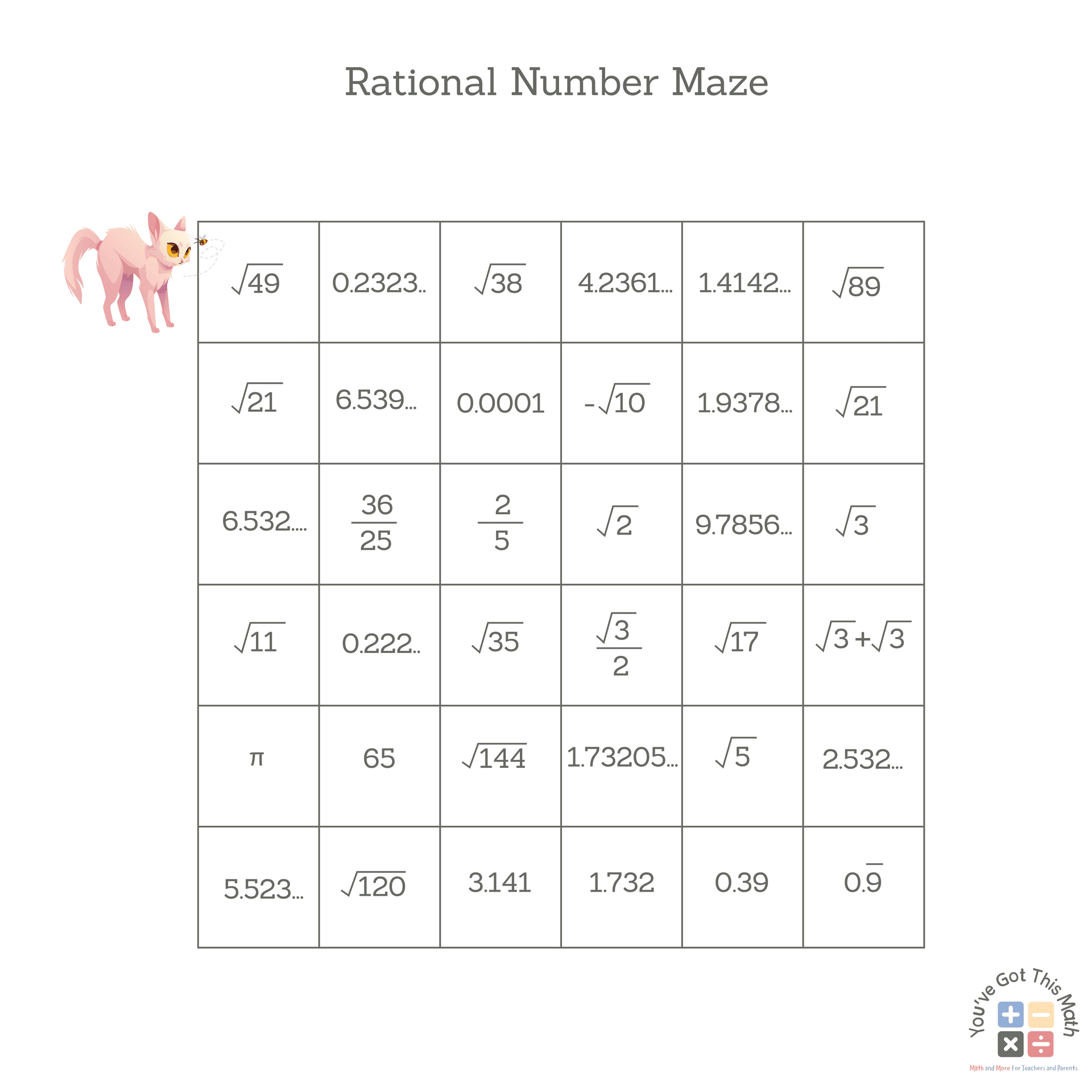
Rational Number Maze
In this activity, we will find out the rational numbers and discover a pattern to let the cat get out of the maze and find its desired food. From the start position, we highlight the numbers that are rational and find a pathway for the cat to move. This activity will help us recognize rational numbers from irrational numbers. This activity is shown in detail as follows:
Irrational Numbers Riddle
Who doesn’t love riddles? What if, with the help of riddle answers, we can learn some rational and irrational numbers? In this activity, we will present some riddles. Each letter or alphabet is assigned an irrational number. With the help of the numbers, we will identify the alphabet and find the answers to the riddles. Let’s get on with it!
Frequently Asked Questions on Rational and Irrational Numbers
1. Is 2 a rational number?
Ans: Since 2 is an integer that can be expressed as 2/1 which satisfies the condition of rational number P/Q where P, Q are integers and Q is not equal to 0, hence, 2 is a rational number.
2. Is √2 a rational or irrational number?
Ans: √2 is an irrational number as √2 = 1.41421356… where the decimal place values do not repeat and are endless. Hence, √2 is an irrational number.
3. Is π a rational or an irrational number?
Ans: π is an irrational number as π = 3.141592… where the decimal place values do not repeat and are endless. Hence, π is an irrational number.
4. Is π equal to 22/7?
Ans: No, although the first two digits of the two numbers are the same, π is an irrational number whereas 22/7 is a rational number. Both 22 and 7 are integers and 22/7 is in the form of P/Q and Q is not equal to zero. 22/7 gives a finite value of decimals but the decimal values for are non-terminating.
5. If a decimal number has a bar above certain digits in the decimal place, then is it a rational number or an irrational number?
Ans: Having a bar above a certain digit after the decimal point means that the certain digit or group of digits is recurring, that is, they will repeat continuously. Hence, such a number is a rational number.
Download This Free Printable PDF
This is the combination of all three worksheets.
So these are our rational and irrational numbers worksheets. Hope this worksheet will help the students to get a basic idea of rational and irrational numbers and also grow proper number sense in them. Please, download the worksheets and give them to the students for practice.
Hello there! I am Mohammad Abrar Uddin and I am an Engineering Graduate from BUET. I write and design articles related to Math topics in You’ve Got This Math and my job is to make math easy and full of fun for everyone!