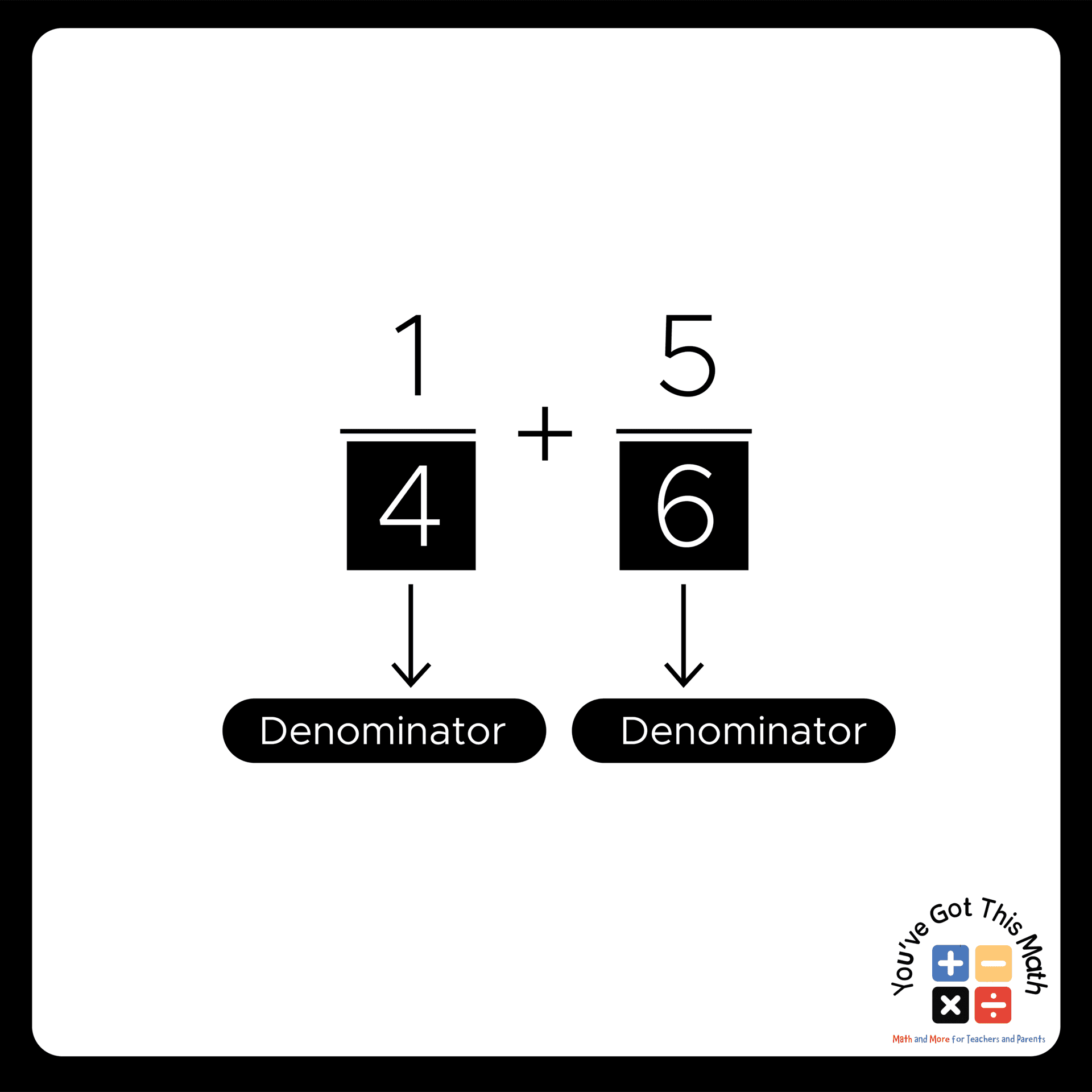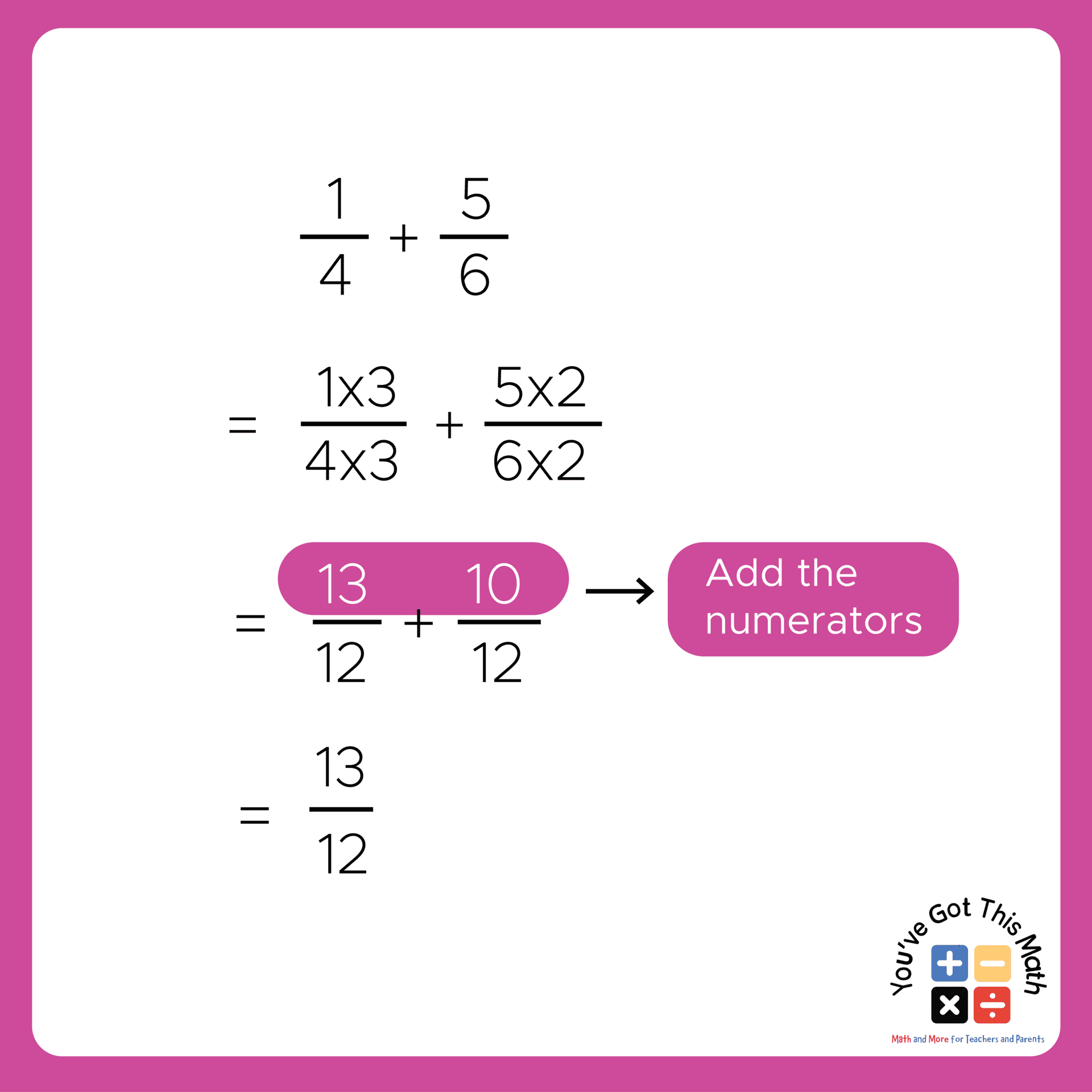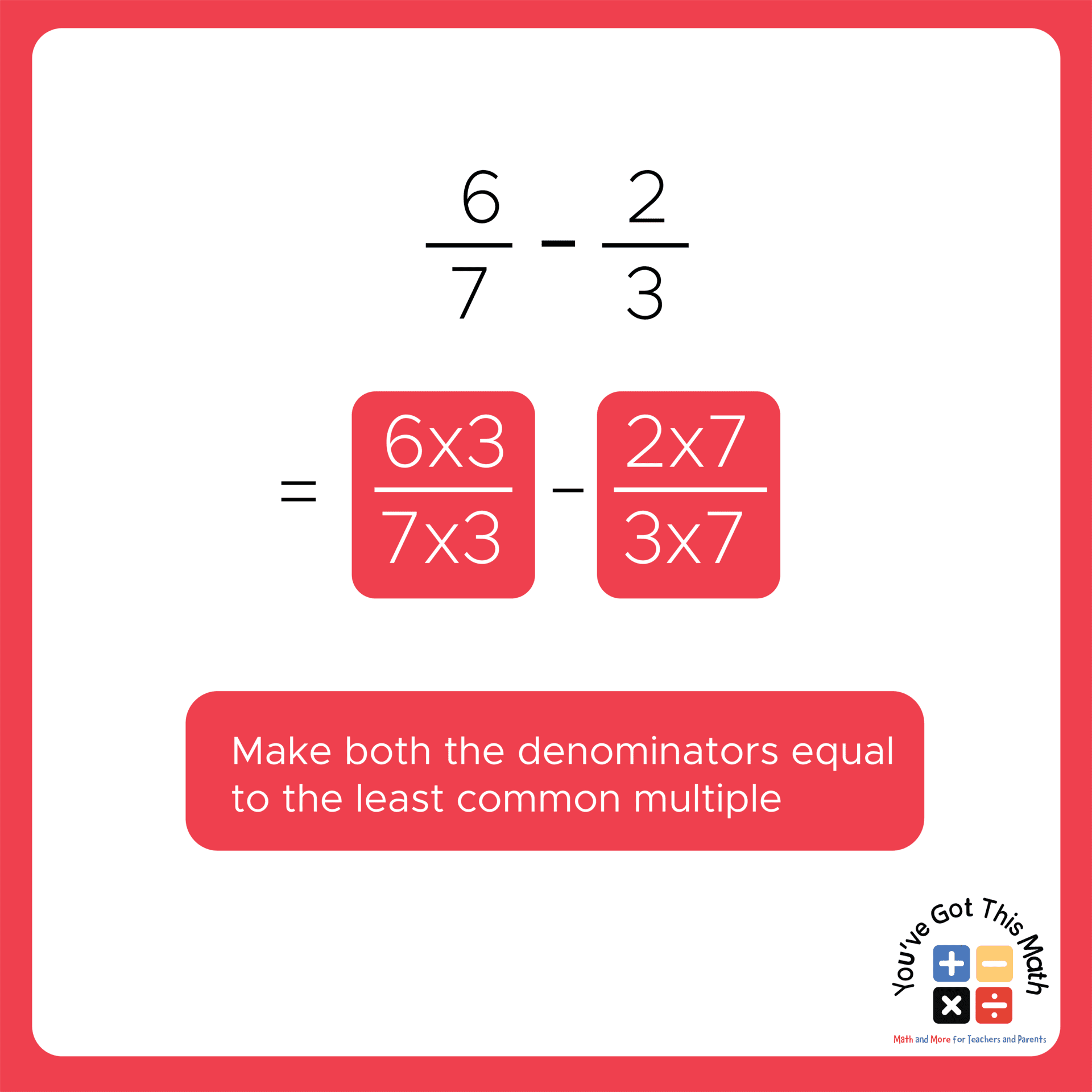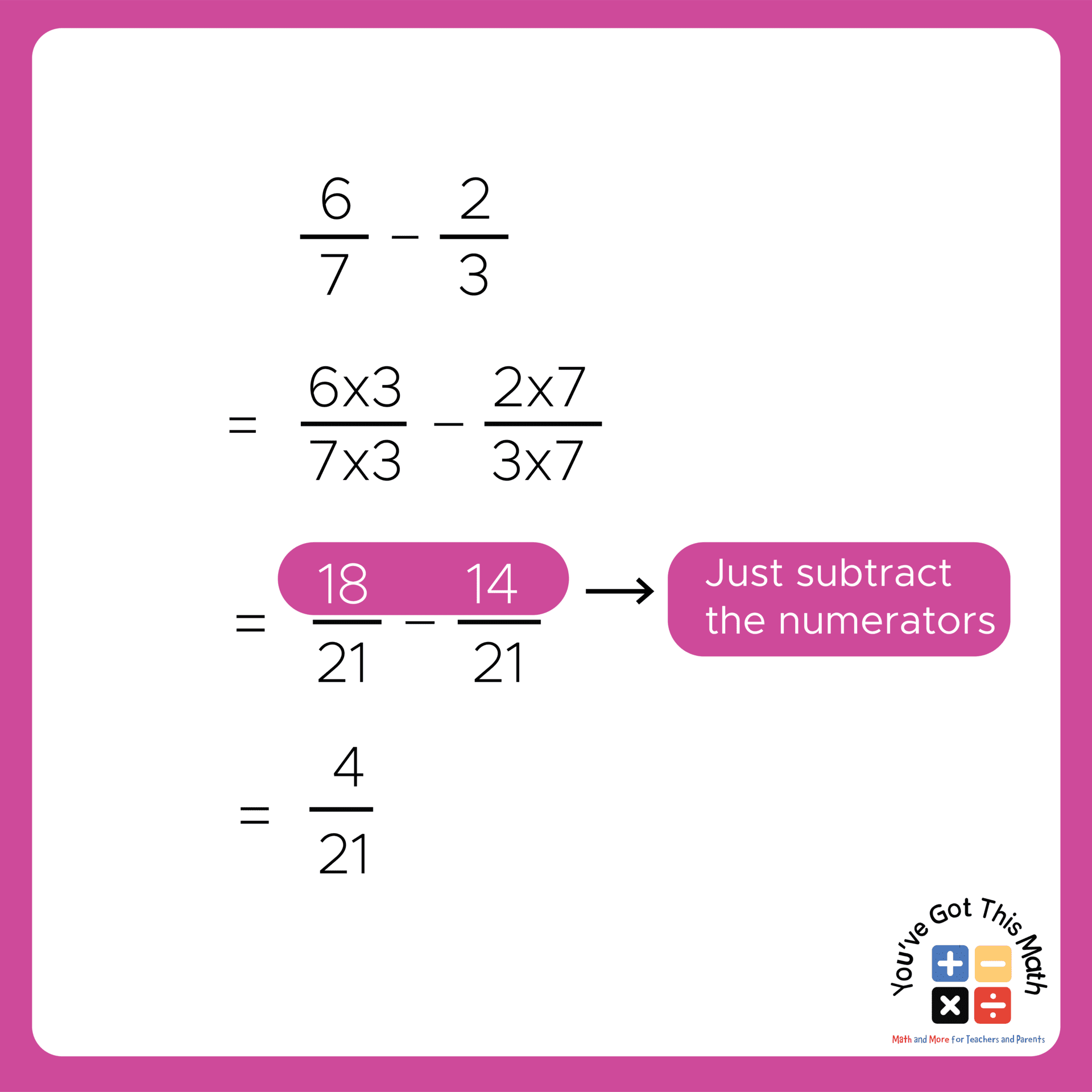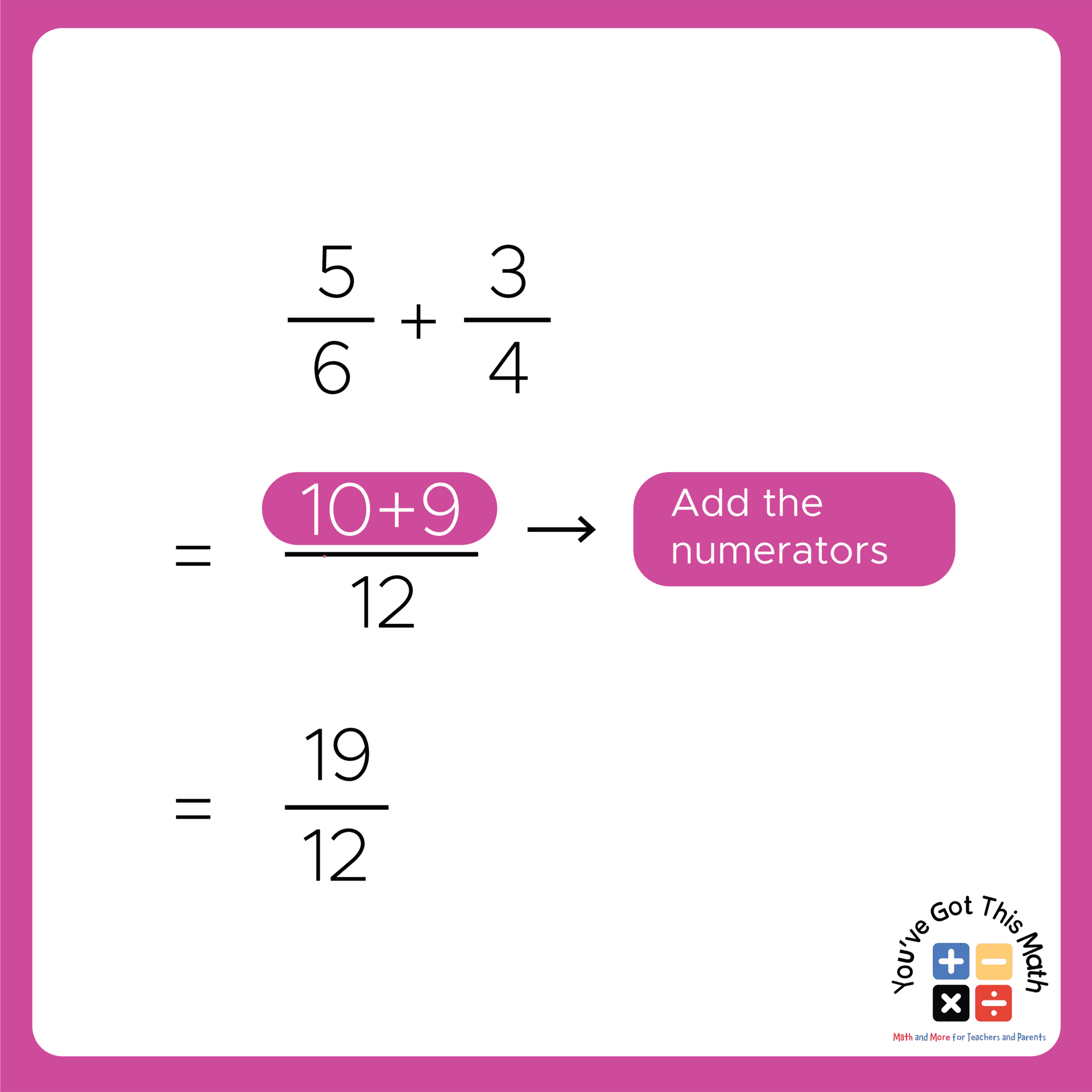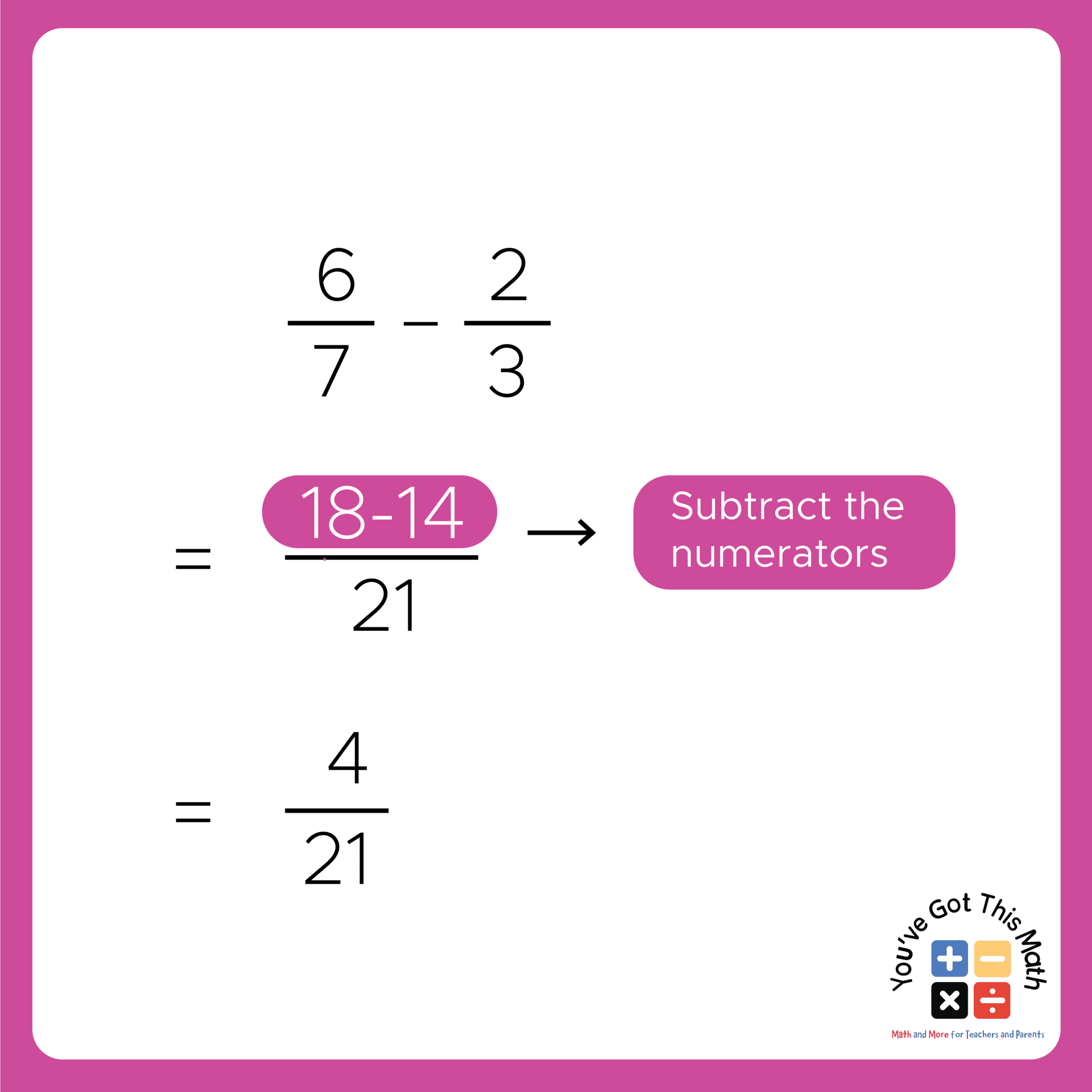How to Add and Subtract Fractions with Different Denominators | 5 Free Worksheets
These how to add and subtract fractions with different denominators worksheets will help to visualize and understand basic mathematical operations with fractions. 5th-grade students will learn basic addition and subtraction methods with fractions and can improve their basic math skills with our free printable adding and subtracting fractions with different denominators worksheets.
5 Free Worksheets to Practice How to Add and Subtract Fractions with Different Denominators
Please download the following fraction addition and subtraction worksheets and practice addition and subtraction of fractions with different denominators on the pages.
Property of Equivalent Fraction
Doing addition and subtraction is fun. But with fractions, we sometimes tend to make mistakes. It’s even harder with fractions with different denominators.
In this discussion, we will learn about fractions, their different properties, and equivalent fractions.
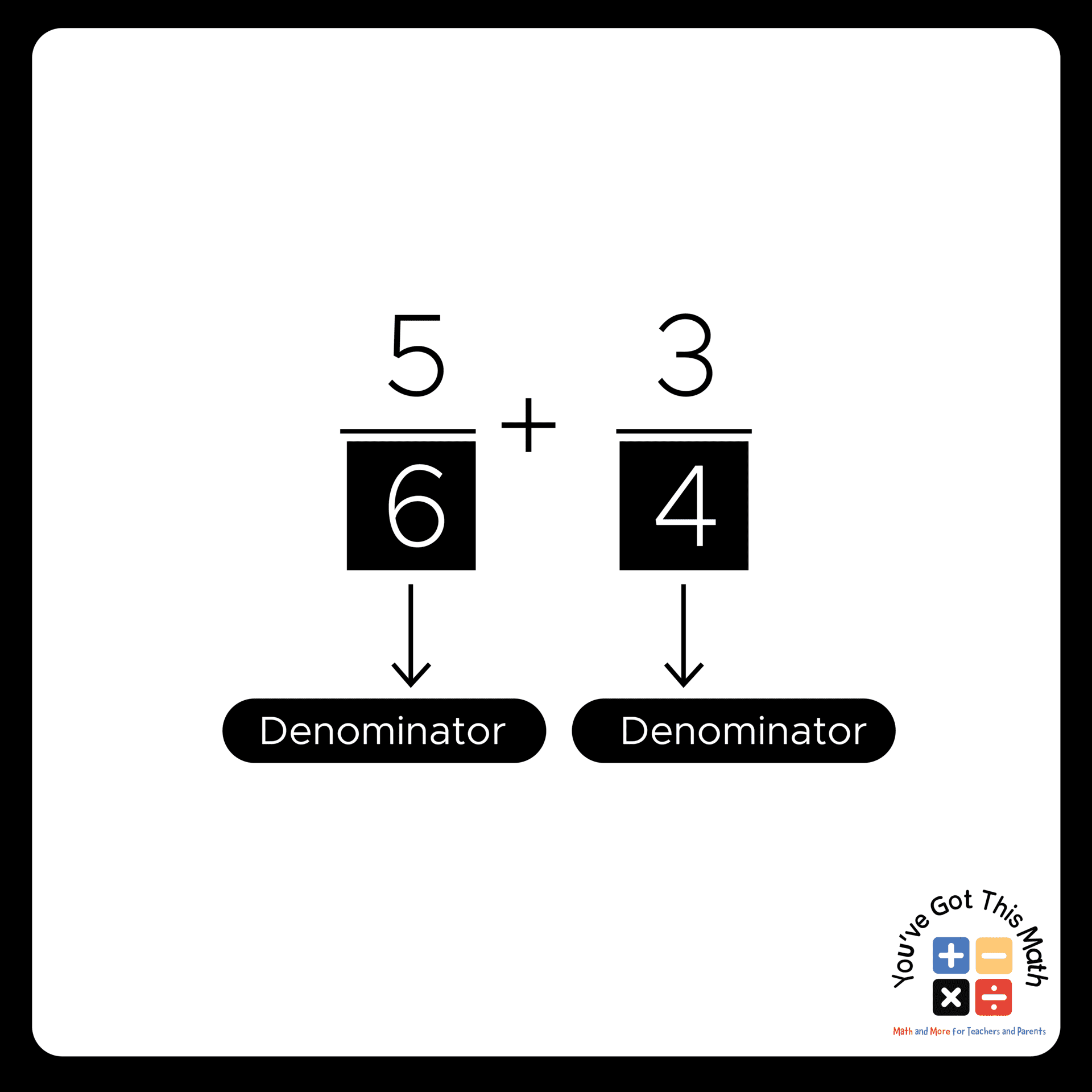
Fraction: We can define a fraction as an integer that is not a whole or full number. We understand 1, 2, 3, 4, etc. as examples of the whole number. But when a number cannot be described as a whole and we have to represent it as a part, the term fraction appears.
We can write a fraction as m/n, where n≠0. The upper part, or m, is called the numerator of a fraction, and the lower part, n, is called the denominator.
As an example of a fraction, we can say that if 5 mangoes out of 10 have been eaten, then 50% or more of the total mangoes have been eaten.
Equivalent Fraction: We will need the term equivalent fraction in our upcoming discussion. Suppose we have a fraction m/n where n≠0 and we will multiply the numerator and the denominator with the same number l where l≠0. So, after multiplying, meaning (mxl)/(nxl) , we will get a new fraction x/y .
Though these two fractions look different, they both have the same value. That means, we can say that m/n = x/y.
3 Effective Methods to Add and Subtract Fractions with Different Denominators
In the following discussion, we will find three effective examples for showing how to add and subtract fractions with different denominators. You will see the use of both equivalent fractions and least common multiples to do the job.
Also, we will demonstrate to you the procedure of adding and subtracting in a single problem. You will also get the idea to add and subtract improper fractions in the later discussion. So, without any further delay, let’s start today’s journey of how to add and subtract fractions with different denominators.
Example 1: Use Common Denominator to Add and Subtract Fractions with Different Denominators
In this method, we will turn the different denominators of the two fractions into a common denominator. How will we do that? We will use an equivalent fraction in this case.
1.1 Adding Two Fractions with Different Denominators
The first procedure will be adding two fractions with different denominators with the help of equivalent fractions. The steps are as follows.
- Take the two fractions for addition.
- Identify the denominators.
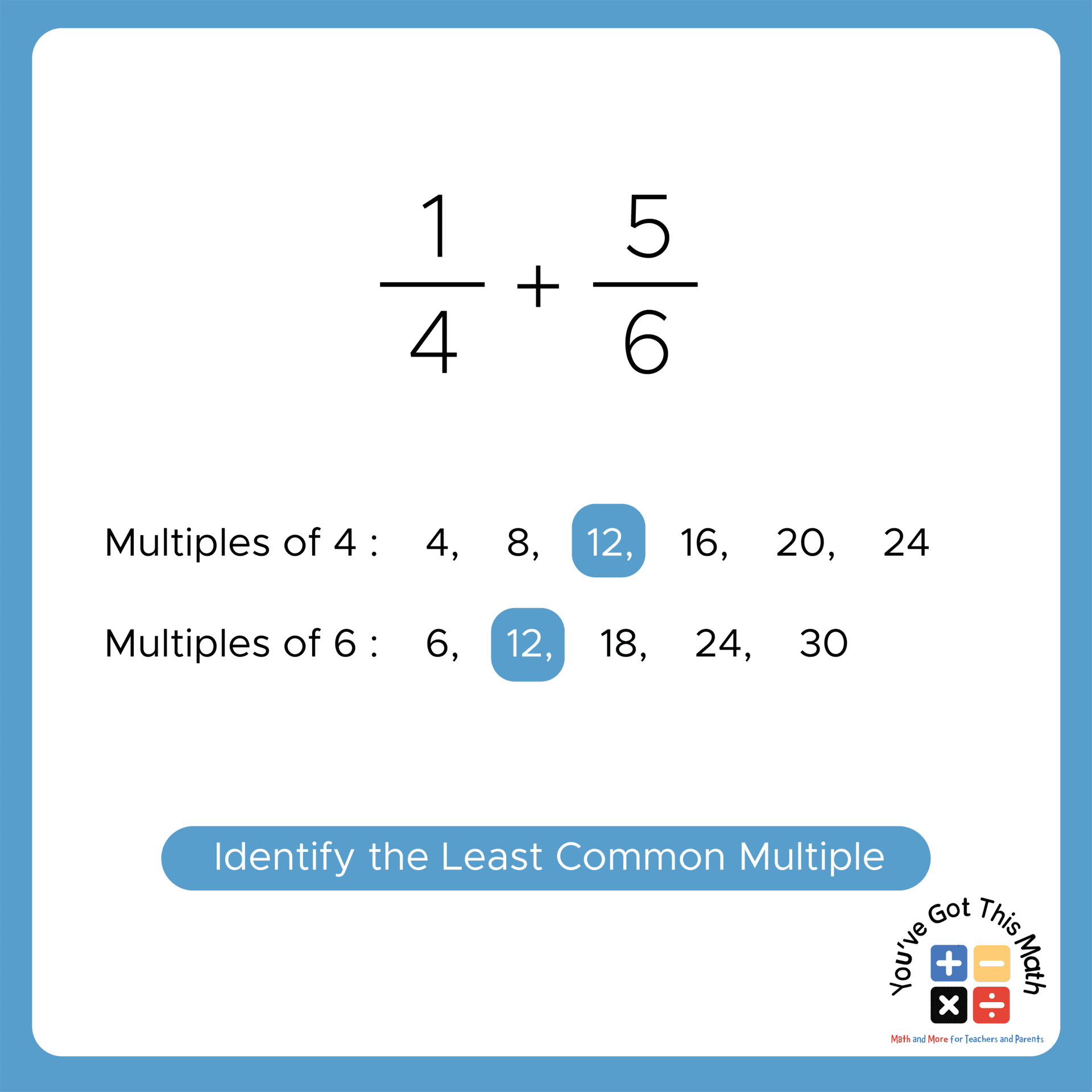
- Then make a list of the multiples of these two denominators.
- For example, in our case, the two denominators are 4 and 6.
- The multiples of 4 are 4, 8, 12, 16, 20, 24, 28, etc.
- The multiples of 6 are 6, 12, 18, 24, 30, 36, etc.
- After that, look for the lowest common multiples from the set of two multiples.
- Here, 12 and 24 are both common in sets of two multiples, but as 12 is the lowest between 2, we will take 12.
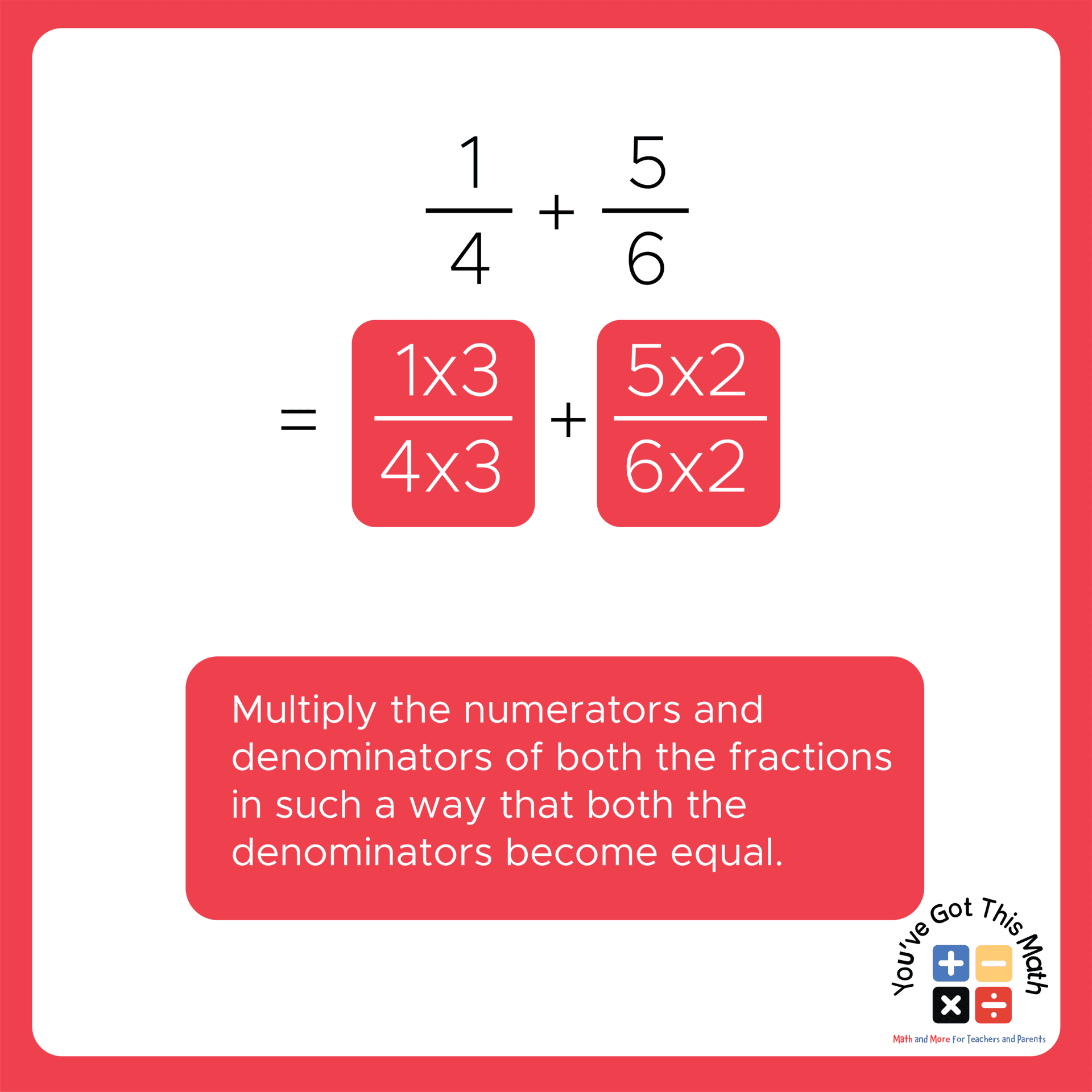
- Now, we will rewrite the two fractions into their equivalent fractions, where both denominators will be 12.
- For that, we will multiply the numerator and denominator of both fractions so that their denominator will be 12.
- For example, for the first fraction, if we multiply the numerator and the denominator by 3 then the denominator will be 12.
- And for the second fraction, multiplying the numerator and the denominator by 2 will make the denominator 12.
- As both the denominators are the same, keep the denominators the same, and add the numerators.
- Here, the numerators are 1 and 5. After multiplying by the designated factor, they have turned into 3 and 10.
- So, after adding 3 and 10, we get 13.
- At last, adding the fraction will result in, 13/12.
1.2 Subtracting Fractions with Different Denominators
The method for subtracting the fraction is almost the same. You have to follow the following simple steps.
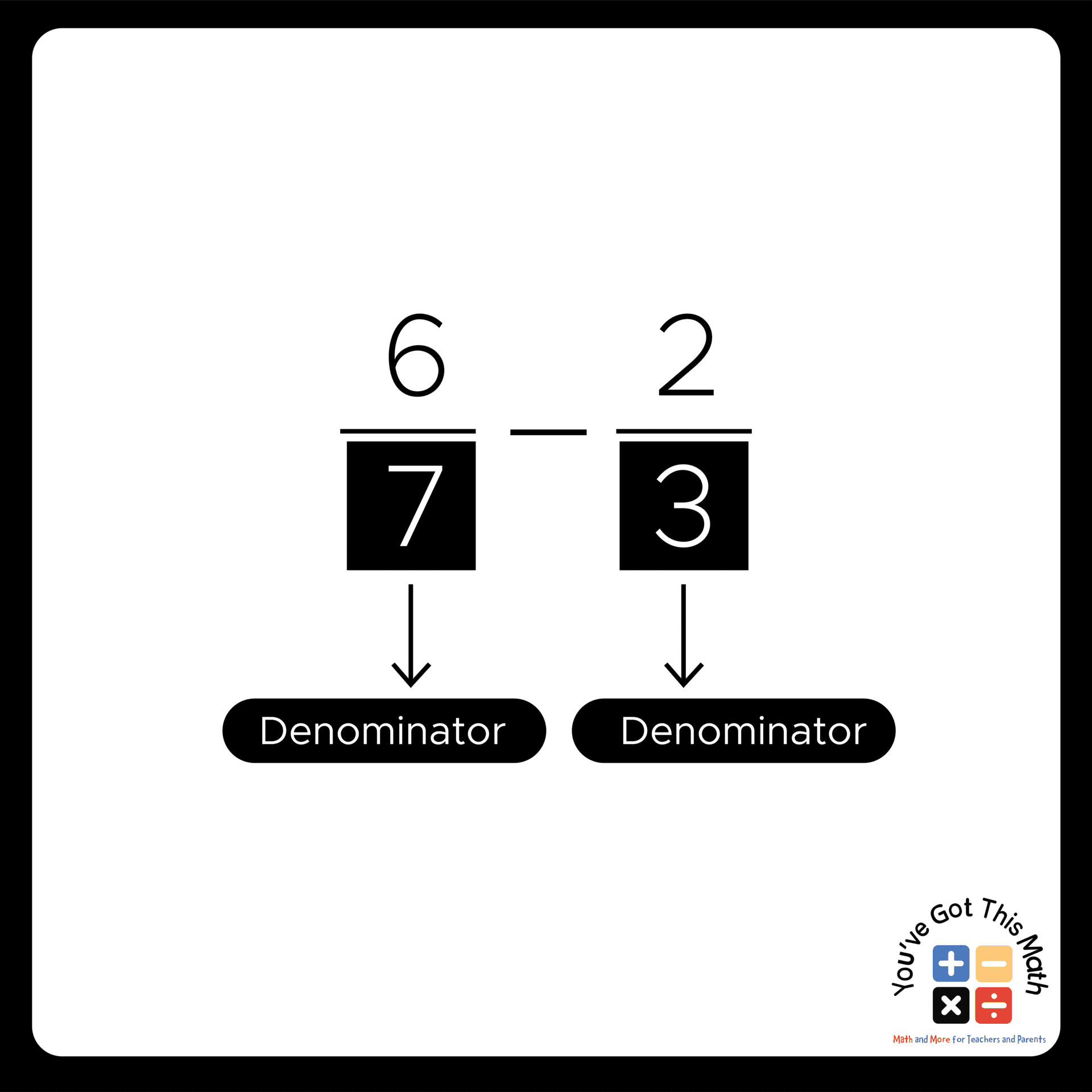
- Take the two fractions for subtraction and identify the denominators.
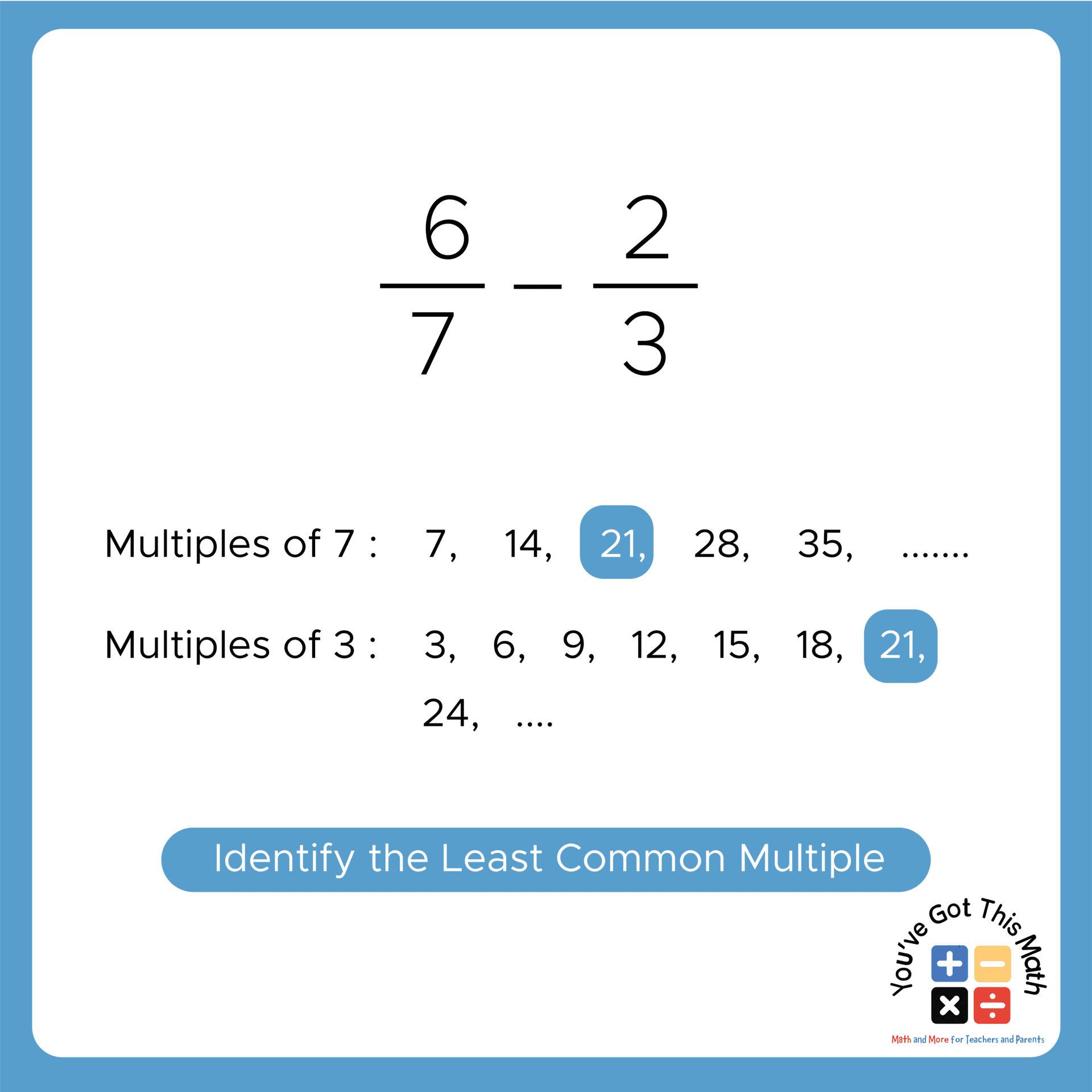
- Again find the least common multiple for the above two denominators, just like in the previous method.
- As the denominators here are 7 and 3, their least common multiple will be 21.
- After that, multiply the numerator and denominator of both fractions to make them 21.
- Finally, keeping the denominator the same, just subtract the numerators, which will result in 4 for our example.
- At last, the subtraction of the fraction will result in, 4/21.
Example 2: Apply Least Common Multiple (LCM) Method to Add and Subtract Fractions with Different Denominators
The second method will enlighten us on the use of the least common multiple (LCM) to add and subtract fractions with a common denominator.
2.1 Adding Two Fractions with Different Denominators
First, we will see the process of adding two fractions with different denominators with the help of the least common multiple. The steps are as follows.
- Take the two fractions for addition.
- Identify the denominators.
- Then determine the multiples of the denominators.
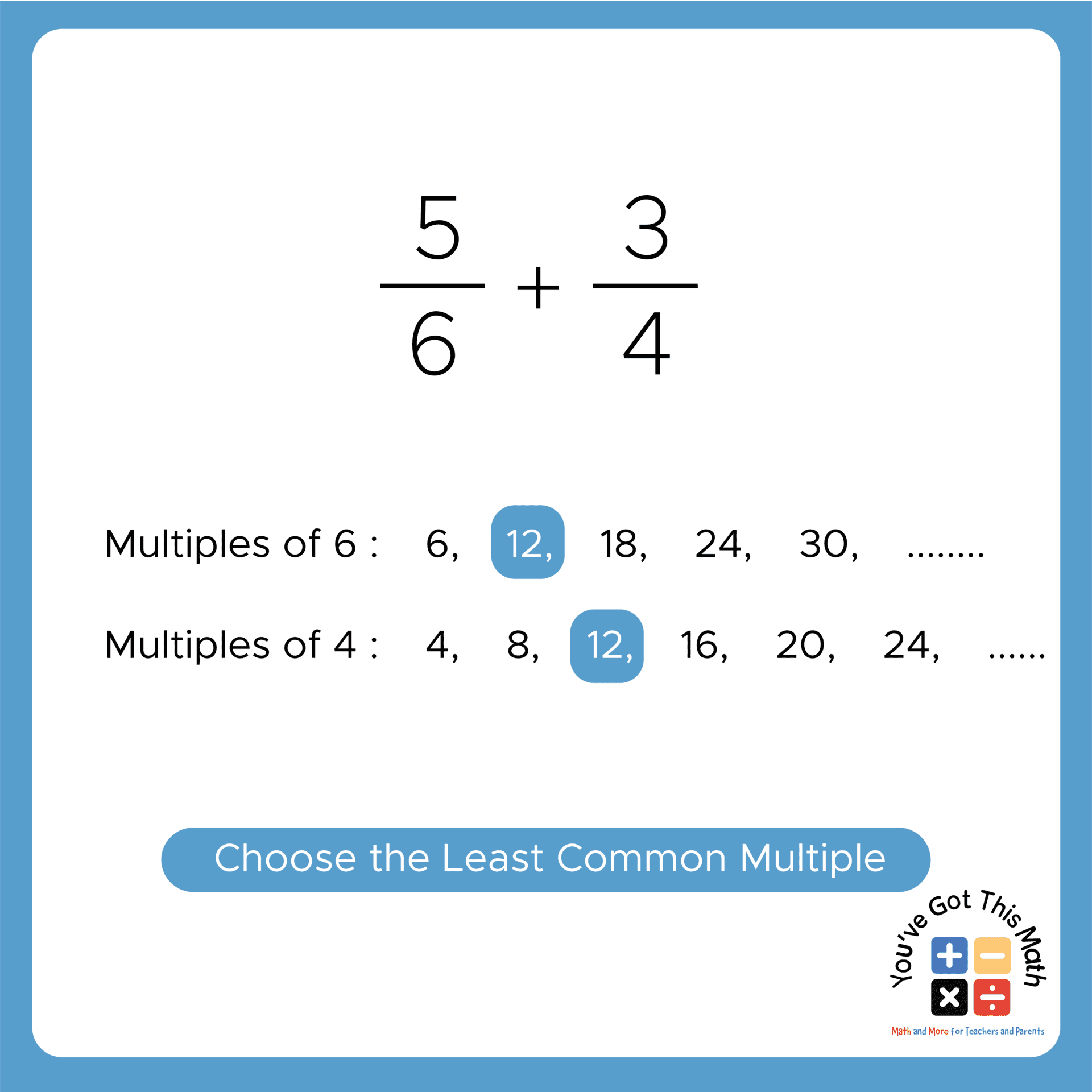
- In our example, the denominators of the two fractions are 6 and 4, respectively.
- The multiples of 6 are 6, 12, 18, 24, 30, 36, etc.
- The multiples of 4 are 4, 8, 12, 16, 20, 24, 28, etc.
- So, we will choose 12 as the common multiple as it is the least common among all the common multiples.
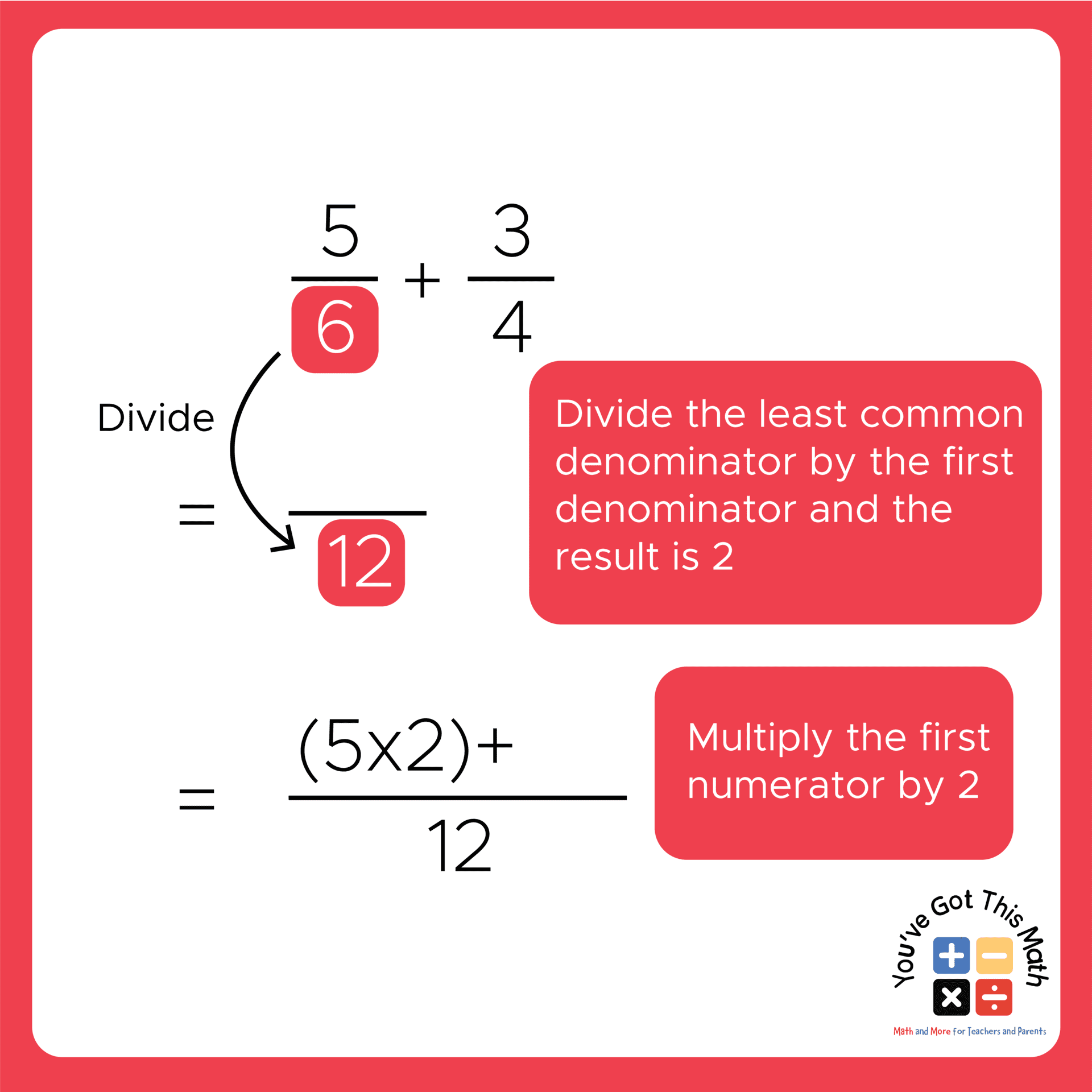
- Now, draw a line and write 12 in the lower part of the line.
- Then take the first denominator (6) and divide 12 by it. We get 2 as the result.
- Now, multiply the first numerator by 2, and we will get 10. Write 10 on the upper part of the line and add a plus sign.
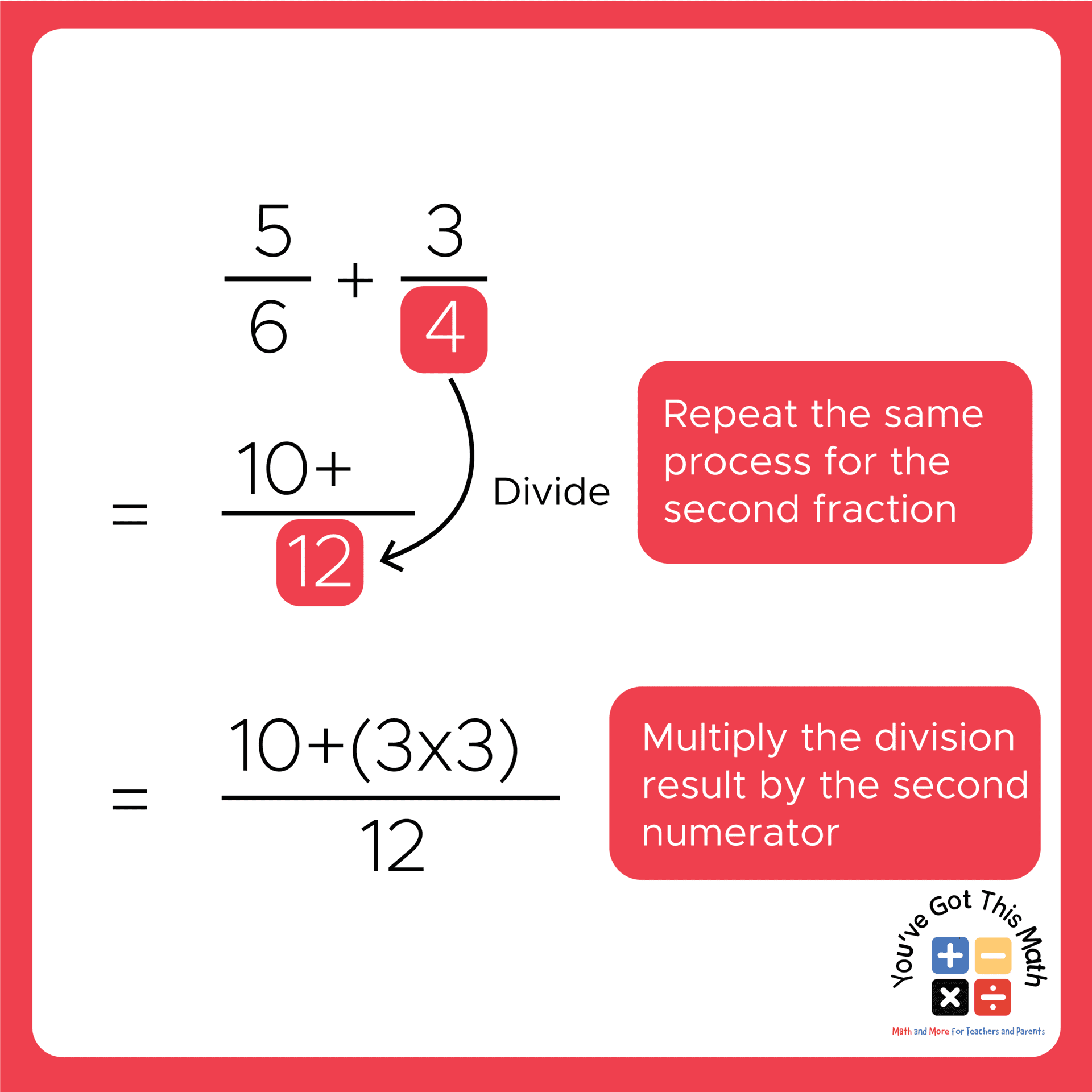
- Again, divide 12 by the second denominator, and this time you will get 3 as the result.
- Now, multiply 3 by 3 which is the second numerator, and write 9 after the plus sign.
- Do the addition of the newly found numerators as in the previous way, and you will get 19 as the addition result.
- At last, adding the fraction will result in, 19/12.
2.2 Subtracting Fractions with Different Denominators
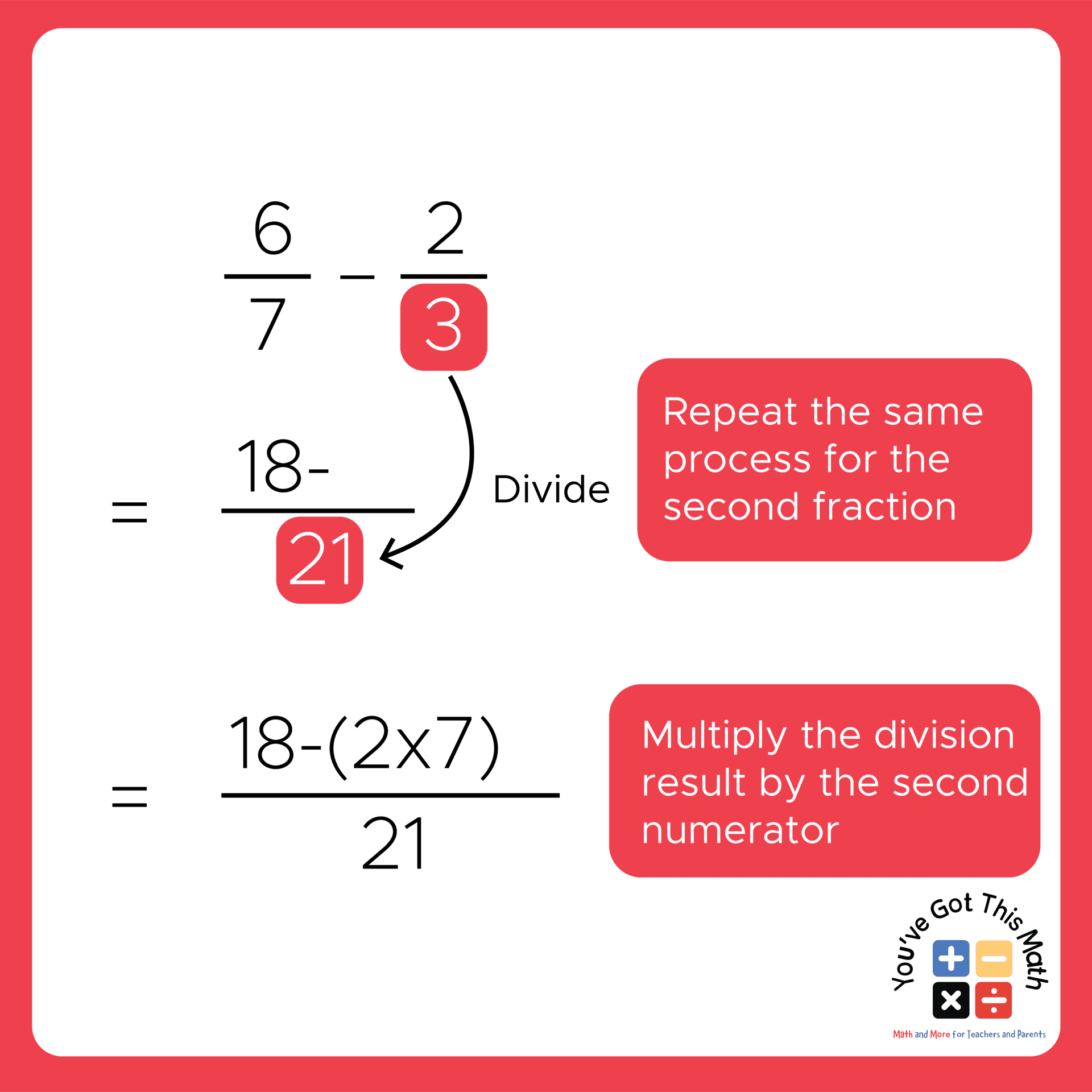
The method for subtracting the fraction with a least common multiple is almost the same as the previous one. Go through the following simple steps.
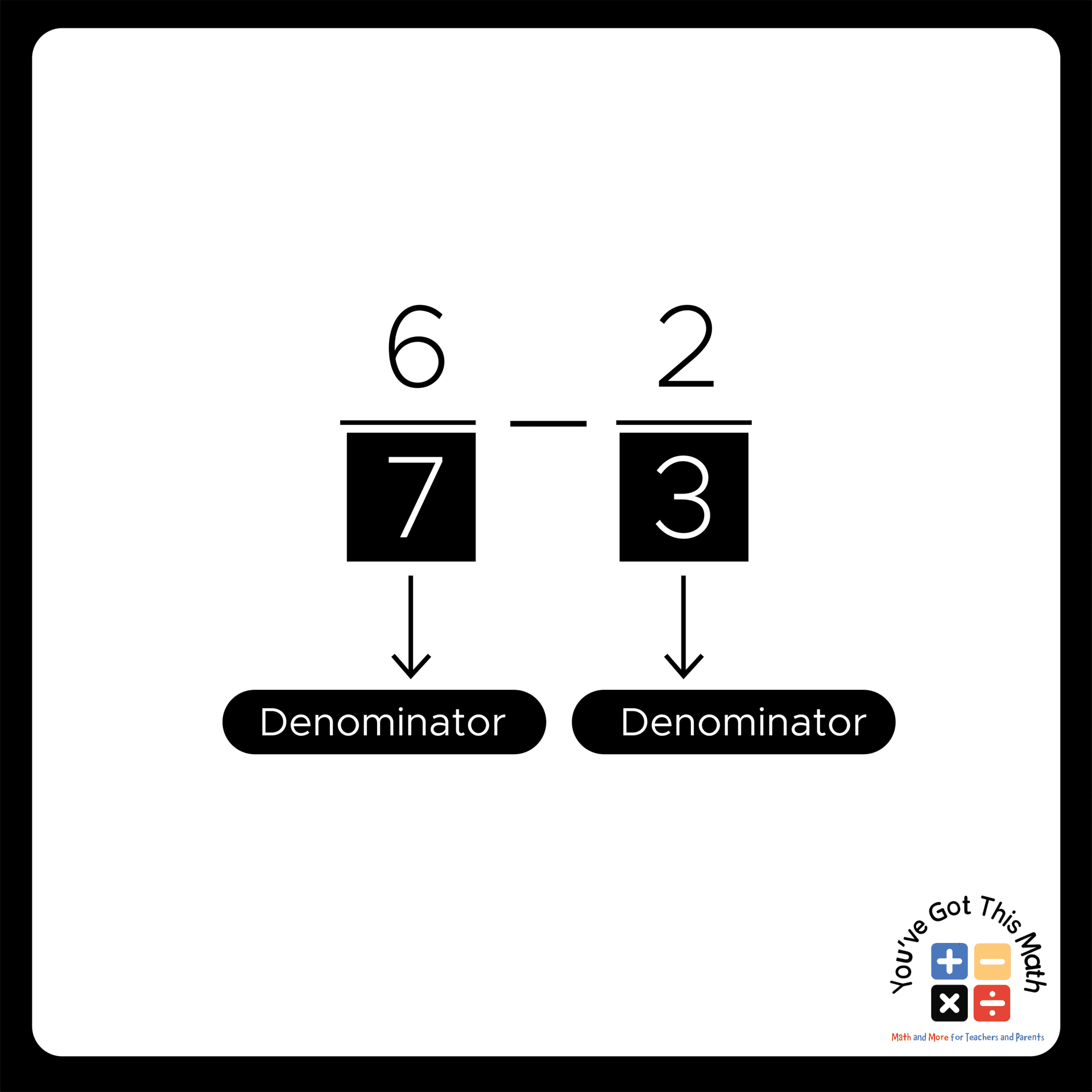
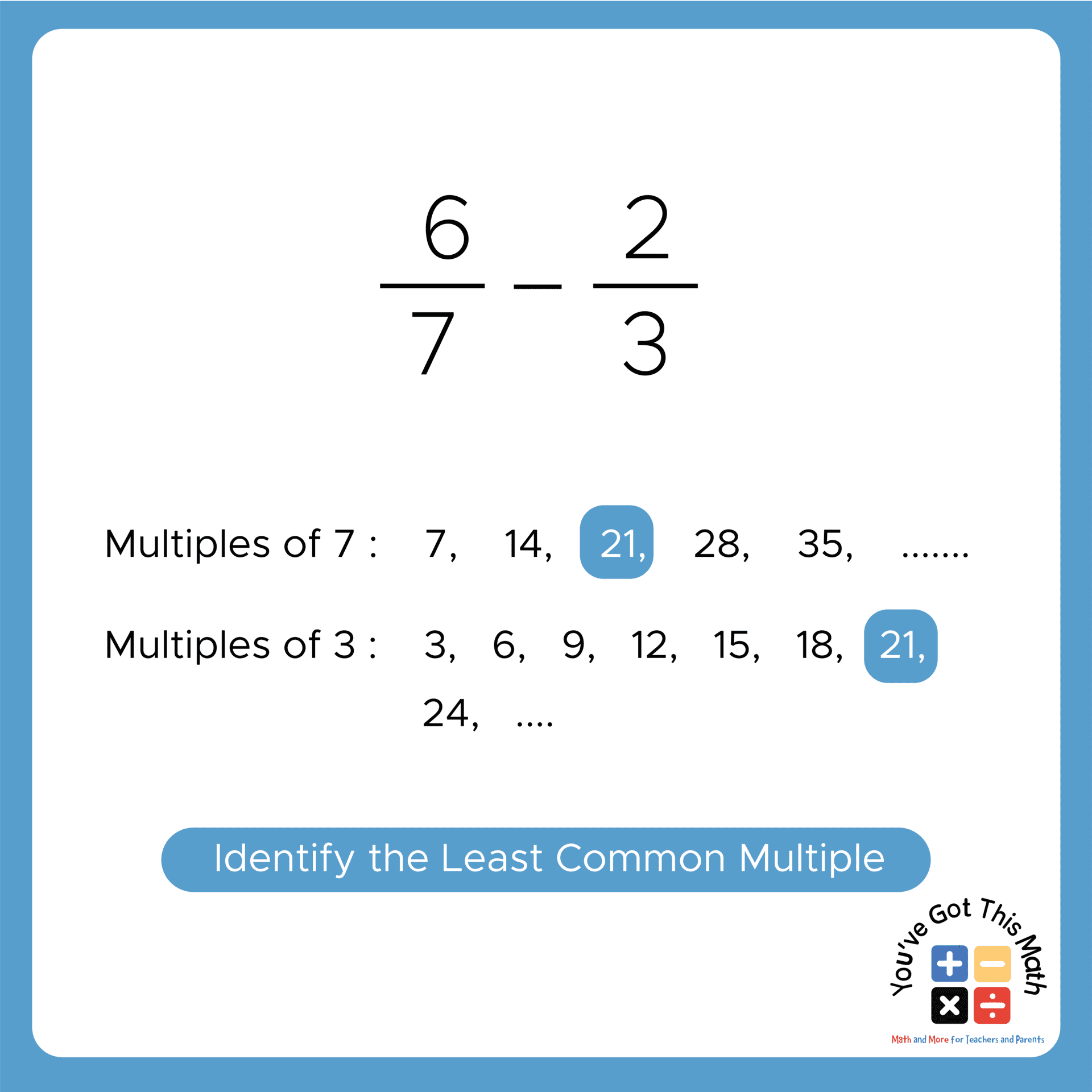
- Take the two fractions for subtraction and identify the denominators.
- Again, find the least common multiple for the above two denominators, just like in the previous method.
- As the denominators here are 7 and 3, their least common multiple will be 21.
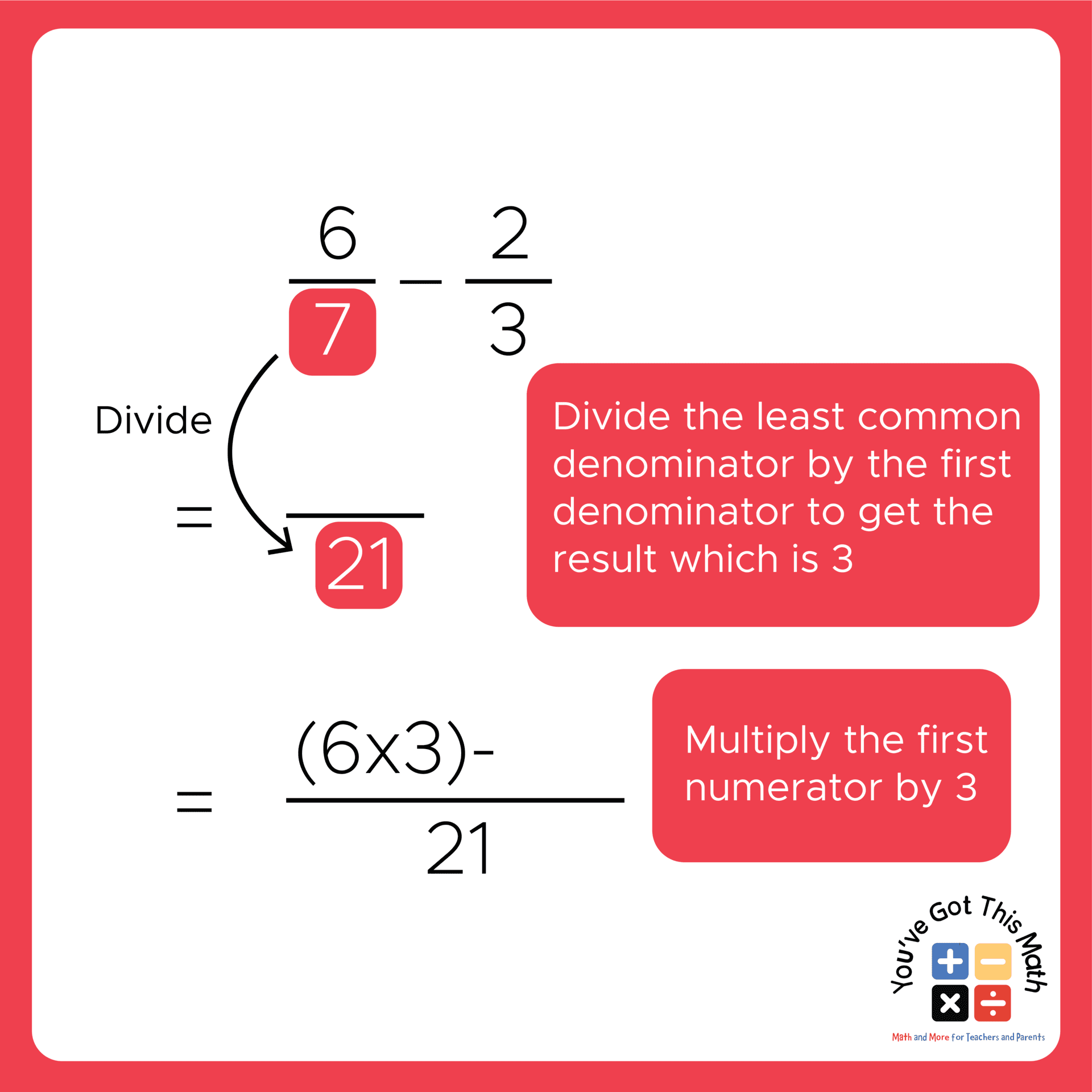
- After that, draw a line and write 21 in the lower part of the line, and just like the previous method, divide 21 by 7, which is the first denominator, and multiply the result of the division by 6, which is the first numerator, and give a minus sign.
- Again, divide 21 by the second denominator, and this time you will get 7 as the result.
- Now, multiply 7 by 2, which is the second numerator, and write 14 after the minus sign.
- Finally, keeping the denominator the same, just subtract the numerators, which will result in 4 for our example.
- At last, the subtraction of the fraction will result in, 4/21.
Example 3: Add and Subtract 3 Fractions with Different Denominators
In this section, we will show you how to do the addition and subtraction of fractions in a single problem. For that, we will require more than two fractions with different denominators. See the below-given easy and simple steps below.
- Firstly, take the problem of simplification and note all the denominators.
- Then, find the LCM of the given denominators, draw a line, and write the LCM in the lower part of the line.
- As explained in Example 2, now divide the LCM with each of the denominators of the fractions given in the problem and multiply the result with their numerators, respectively.
- Afterward, we will write the results of the multiplication one by one on the upper part of the line.
- Then, for ease of calculation, keep the addition part together inside the first bracket and the subtraction part on the other part, or vice-versa.
- Add the parts inside the bracket, then write the result. If there are two subtractions and one addition in your problem, then you have to keep the subtraction part together inside the bracket.
- At last, subtract the part from the addition result of the previous step and find the answer to this simplification.
Example 4: Add and Subtract Mixed Numbers with Different Denominators
In this discussion, we will show you how to do addition and subtraction with improper fractions. In many cases, improper fractions are given as mixed numbers. What will be our procedure in this regard is given in the following steps.
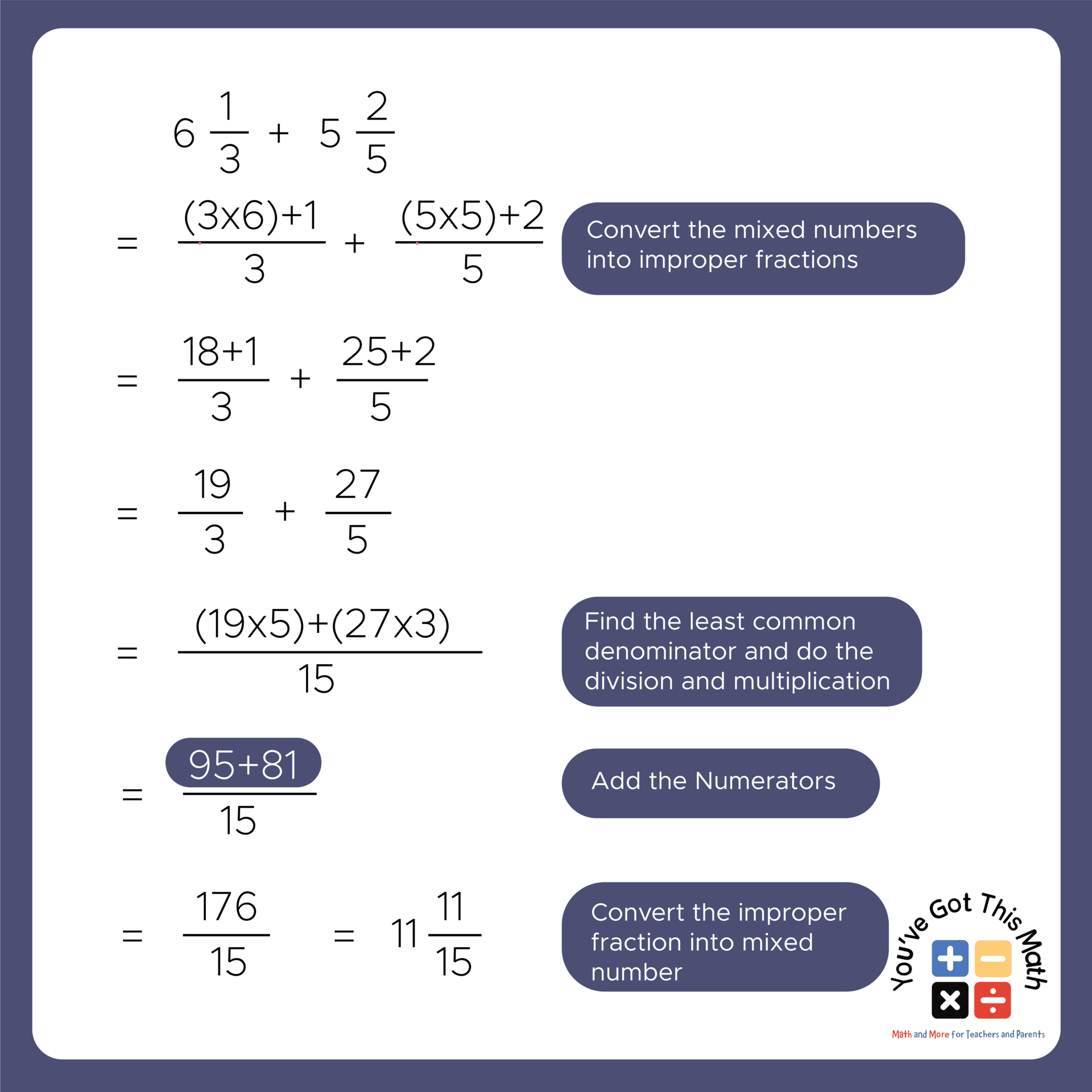
- First, see the given mixed numbers and turn them into improper fractions.
- Then, find the LCM of the given denominators of the improper fractions, draw a line, and write the LCM in the lower part of the line.
- As explained in Example 2, now divide the LCM with each of the denominators of the fractions given in the problem and multiply the result with their numerators, respectively.
- Afterward, we will write the results of the multiplication one by one on the upper part of the line.
- At last, do addition or subtraction as per the given problem and find the answer.
Add and Subtract Fractions with Like Denominators
Our last discussion will focus on adding and subtracting fractions that have the same or like denominators. The following steps will help you in this regard.
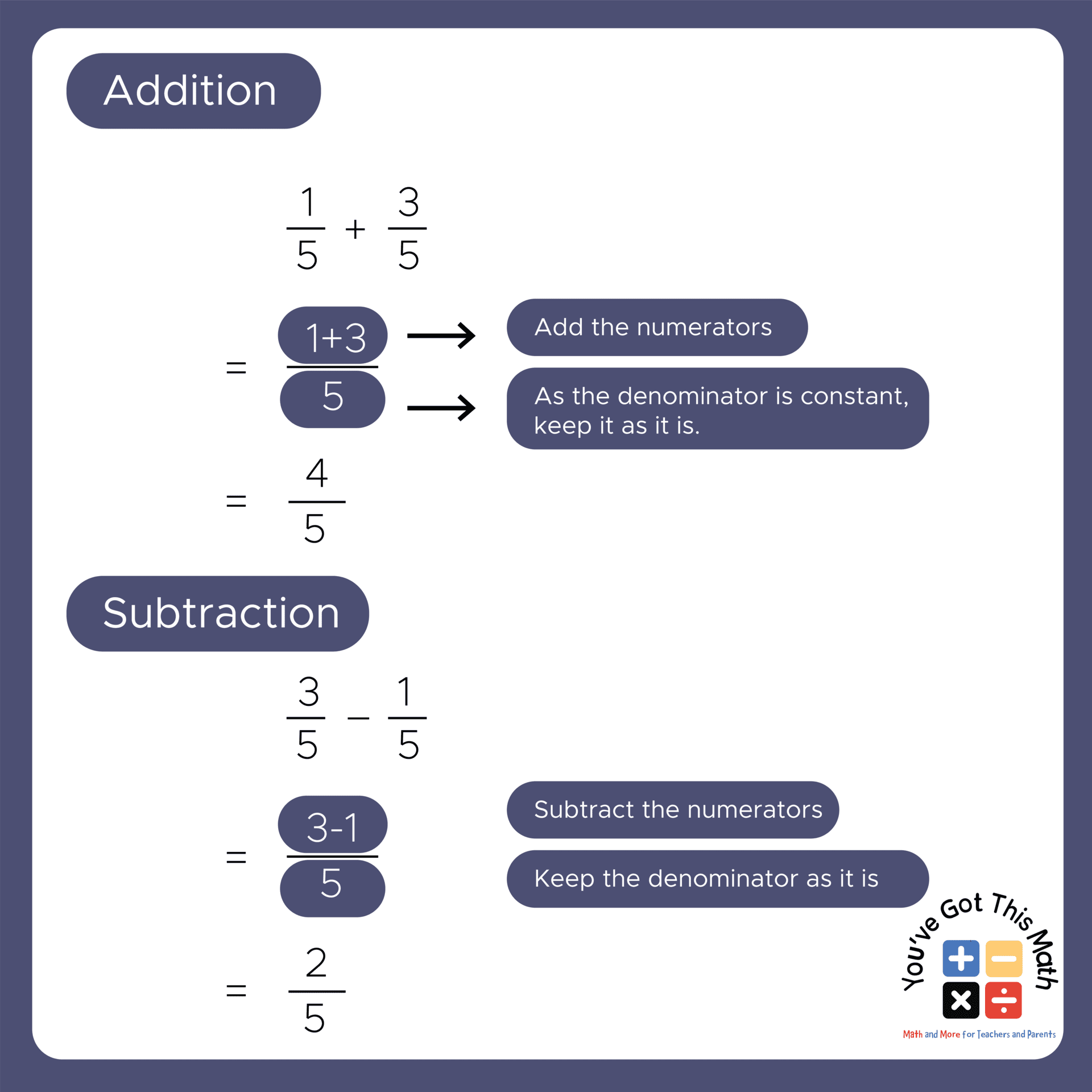
- First, note the fractions with the same denominators.
- As the denominators are the same, you don’t have to find any LCM or turn the fractions into equivalent ones.
- Just see the numerators and the operation sign, whether it is a plus or minus.
- After that, simply add or subtract the numerator as per the question and write the answer.
- And just like that, you have found the answer to the addition or subtraction of fractions with the same denominators.
Download Free Printable PDF
Download the following combined PDF and enjoy your practice session.
So today, we’ve discussed how to add and subtract fractions with different denominators worksheets using the concepts of fractions, numerator and denominator, addition and subtraction, equivalent fractions, least common multiples, and some interactive addition and subtraction problems. Download our free worksheets, and after practicing these worksheets, students will surely improve their mathematical skills and have a better understanding of addition and subtraction of fractions with different denominators.
Hello, I am Md. Araf Bin Jayed. I have completed my B.Sc in Industrial and Production Engineering from Ahsanullah University of Science and Technology. Currently I am working as a Content Developer for You Have Got This Math at Softeko. With proper guidelines and aid from the parent organization Softeko, I want to represent typical math problems with easy solutions. With my acquired knowledge and hard work, I want to contribute to the overall growth of this organization.