9 Free Improper Fractions to Mixed Numbers Anchor Chart
These improper fractions to mixed numbers anchor chart will help to visualize and understand improper fractions to mixed numbers. 4th grade students will learn basic converting methods and can improve their basic math skills with our free printable improper fractions to mixed numbers anchor chart.
9 Exciting Improper Fractions to Mixed Numbers Anchor Chart Examples
Please download the following improper fractions to mixed numbers anchor chart and practice examples on the pages.
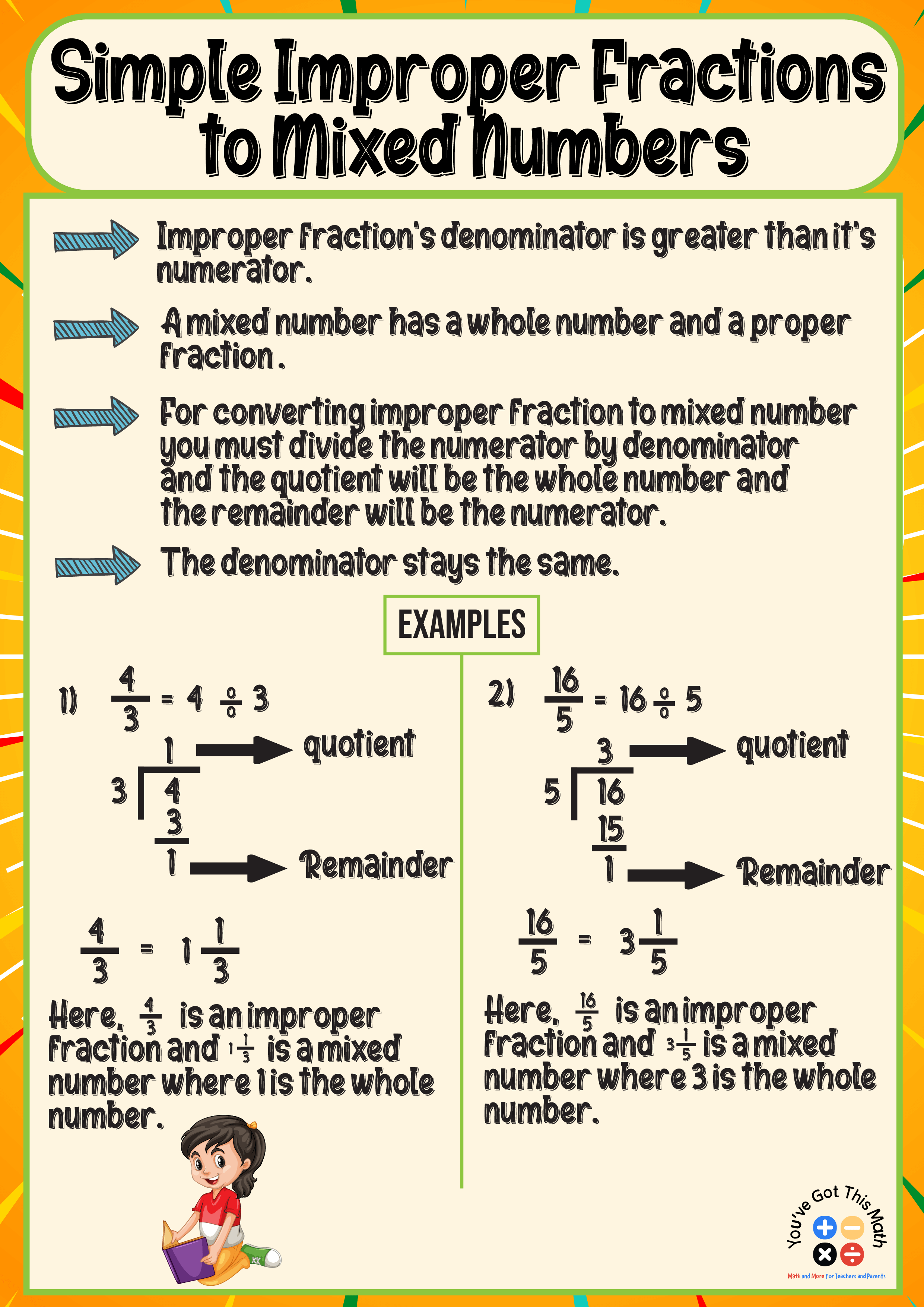
Simple Improper Fractions to Mixed Numbers
This method is about simple problems on converting improper fractions to mixed numbers on an anchor chart to your children.
For example, if a student converts 4/3, first divide the numerator by the denominator.
Here, 4 is the numerator and 3 is the denominator. The quotient is the whole number, the remainder is the numerator, and the denominator stays the same. So after dividing 4 by 3, the quotient is 1, which is the whole number, and the remainder is 1, which acts as the numerator.
The denominator remains the same, which is 3.
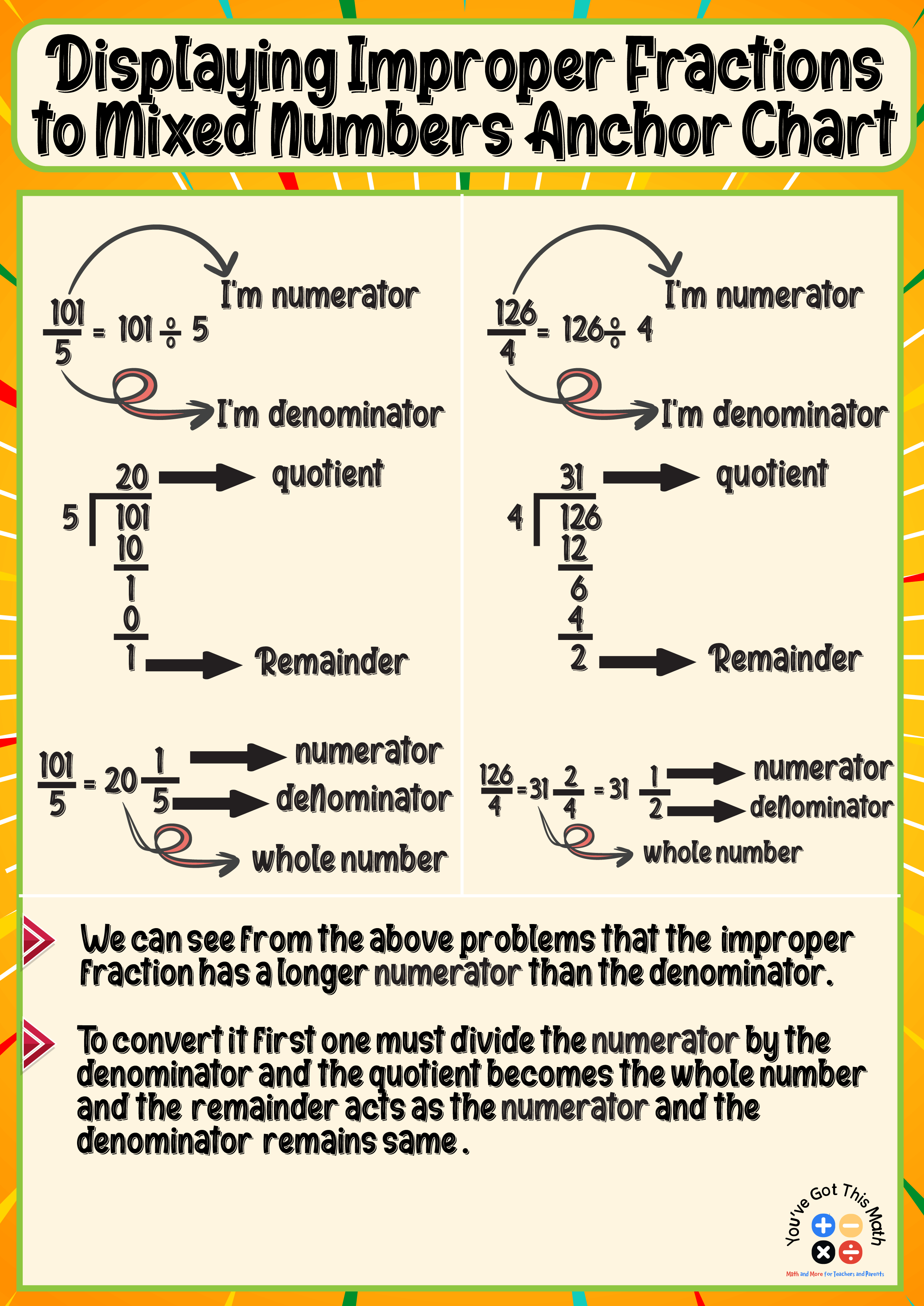
Displaying Improper Fractions to Mixed Numbers Anchor Chart
In this method, they will learn how to convert as well as how to make posters. As an example, if a student converts 101/5, he will first divide the numerator by the denominator. Here, 101 is the numerator, and 5 is the denominator.
The quotient is the whole number, the remainder is the numerator, and the denominator stays the same.
So after dividing 101 by 5, the quotient is 20, which is the whole number, and the remainder is 1, which acts as the numerator. The denominator remains the same, which is 5.
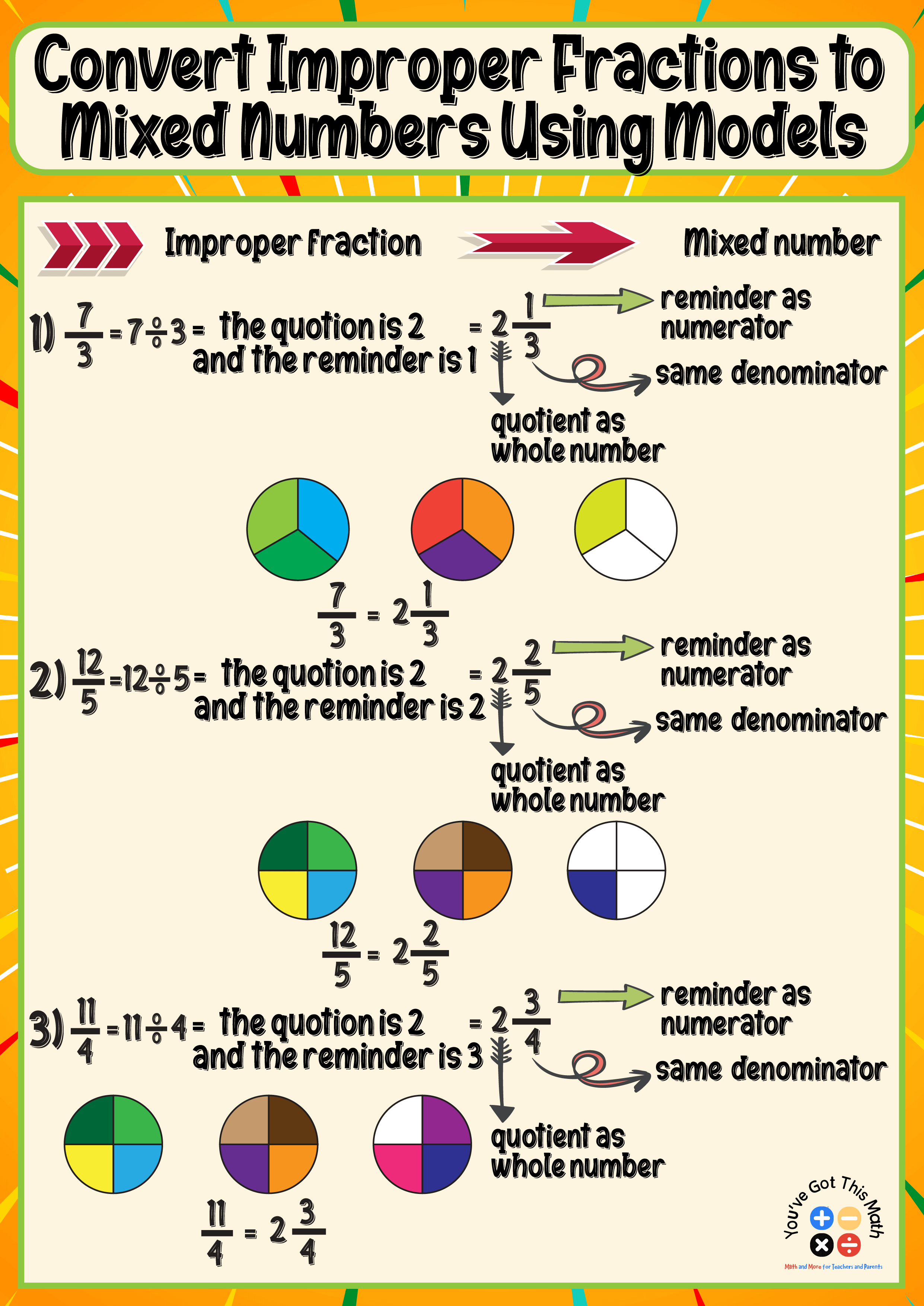
Converting Improper Fractions to Mixed Numbers Anchor Chart with Models
To convert 7/3, a student first divides the numerator by the denominator.
The numerator in this problem is 7, and the denominator is 3. The denominator remains unchanged, the remainder serves as the numerator, and the quotient is the whole number.
As a result, when 7 is divided by 3, the quotient, which is the whole number, is 2, and the remainder, 1, serves as the numerator. The denominator, which is 3, stays the same.
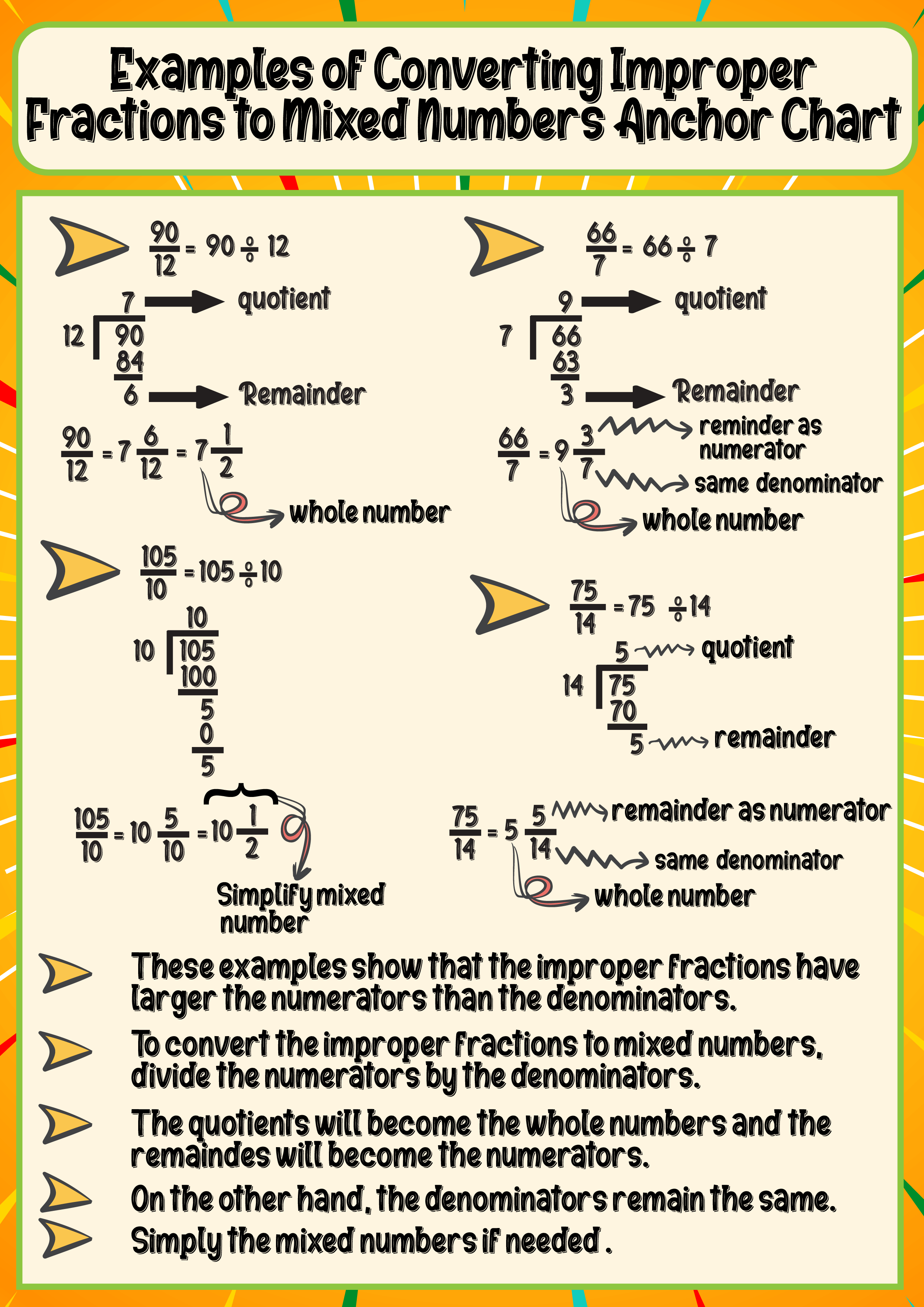
Examples of Converting Improper Fractions to Mixed Numbers Anchor Chart
To convert 90/12, a student first divides the numerator by the denominator.
The numerator in this problem is 90, and the denominator is 12. The denominator remains unchanged, the remainder serves as the numerator, and the quotient is the whole number.
As a result, when 90 is divided by 12, the quotient, which is the whole number, is 7, and the remainder, 6, serves as the numerator. The denominator, which is 12, stays the same.
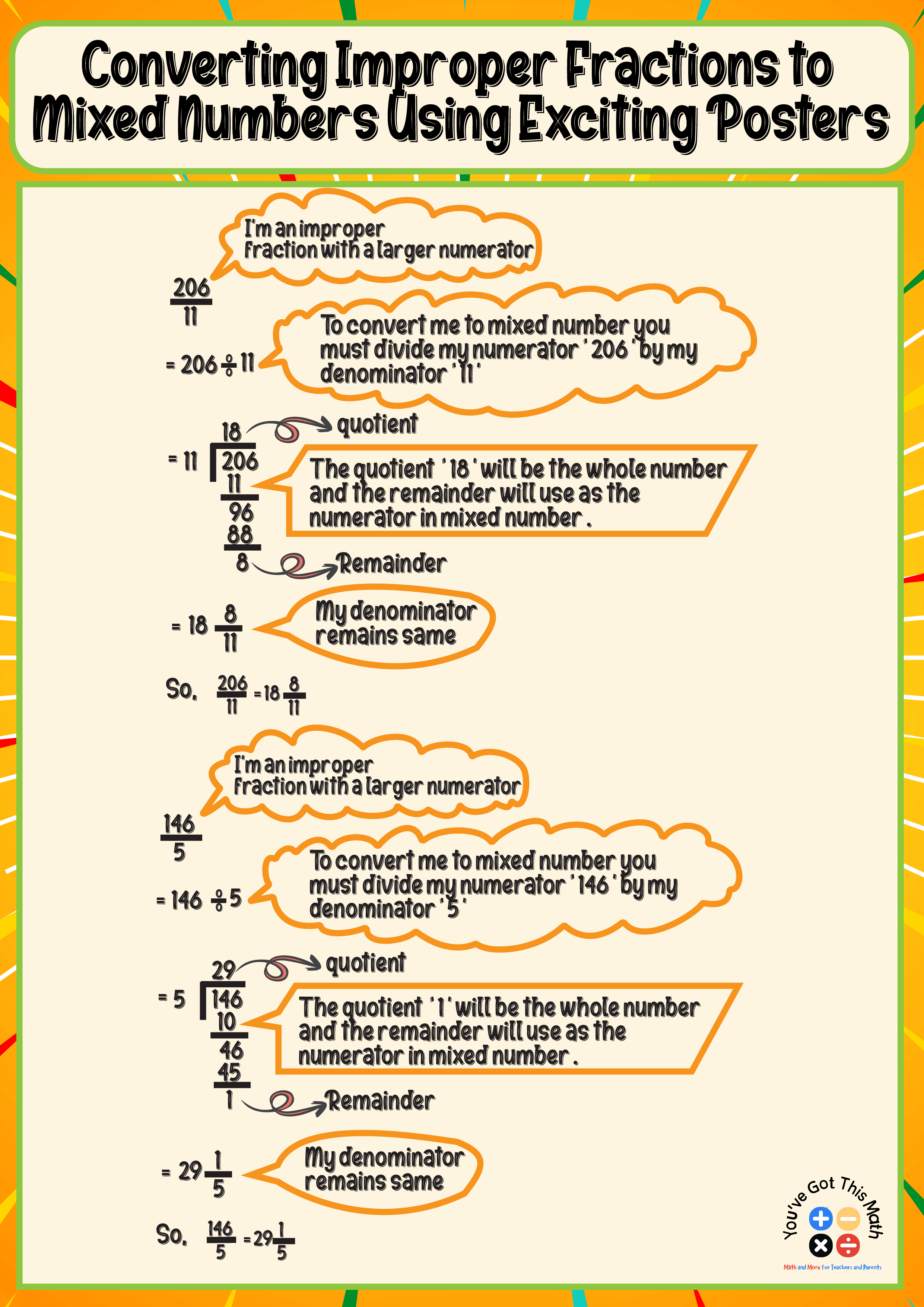
Converting Improper Fractions to Mixed Numbers Using Exciting Posters
To convert 206/11, a student would first divide the numerator by the denominator. The numerator in this equation is 206, and the denominator is 11.
The denominator remains the same, the remainder serves as the numerator, and the quotient is the whole number. As a result, when 206 is divided by 11, the quotient, which is the full number, is 18, and the remainder, 8, serves as the numerator. The denominator, which is 11, stays the same.
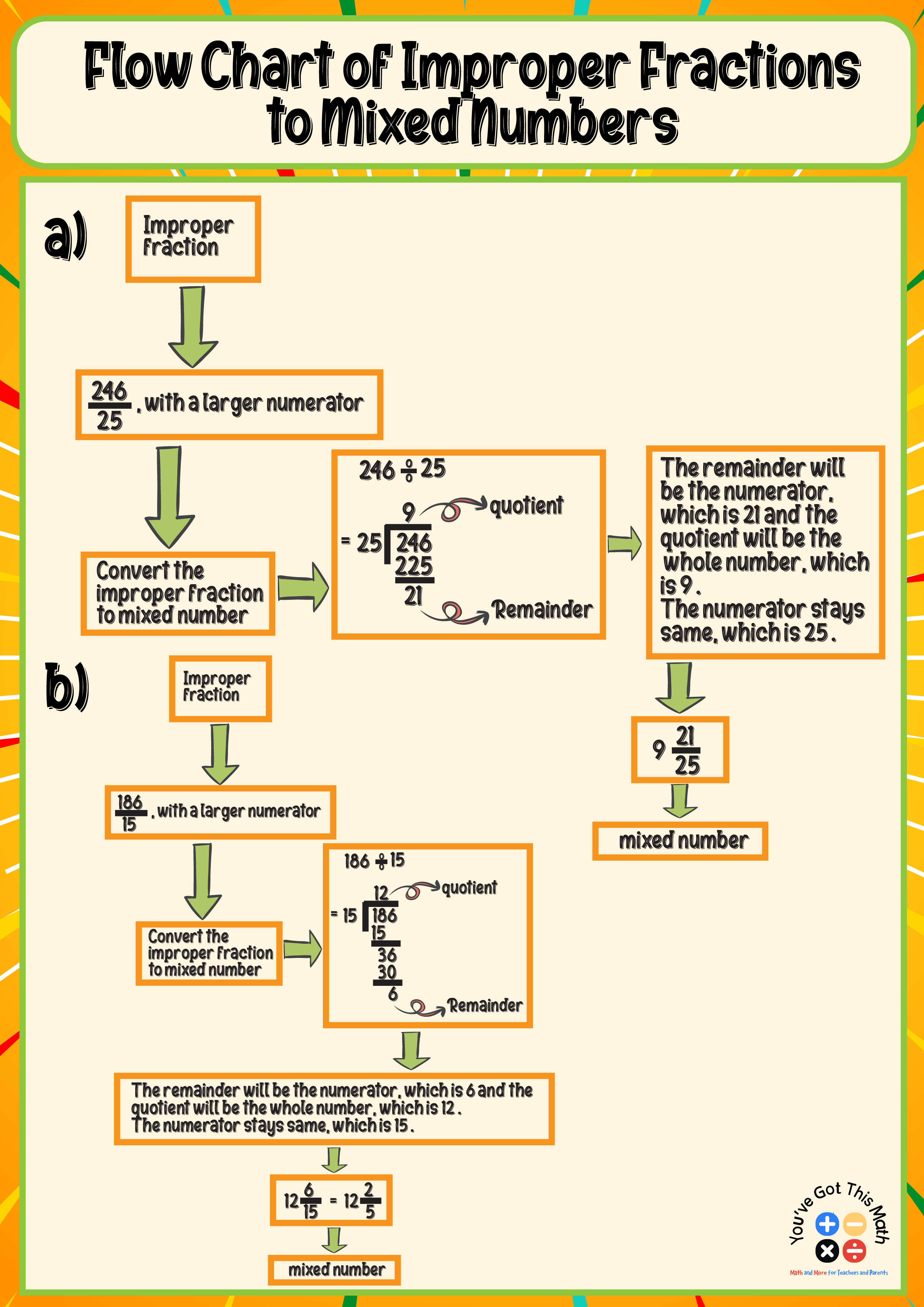
Flow Chart of Improper Fractions to Mixed Numbers
A flow chart can make a difficult problem simpler.
For example, if a student converts 246/25, he will first divide the numerator by the denominator.
Here, 246 is the numerator, and 25 is the denominator. The quotient is the whole number, the remainder is the numerator, and the denominator stays the same.
So after dividing 246 by 25, the quotient is 9, which is the whole number, and the remainder is 21, which acts as the numerator.
The denominator remains the same, which is 25.
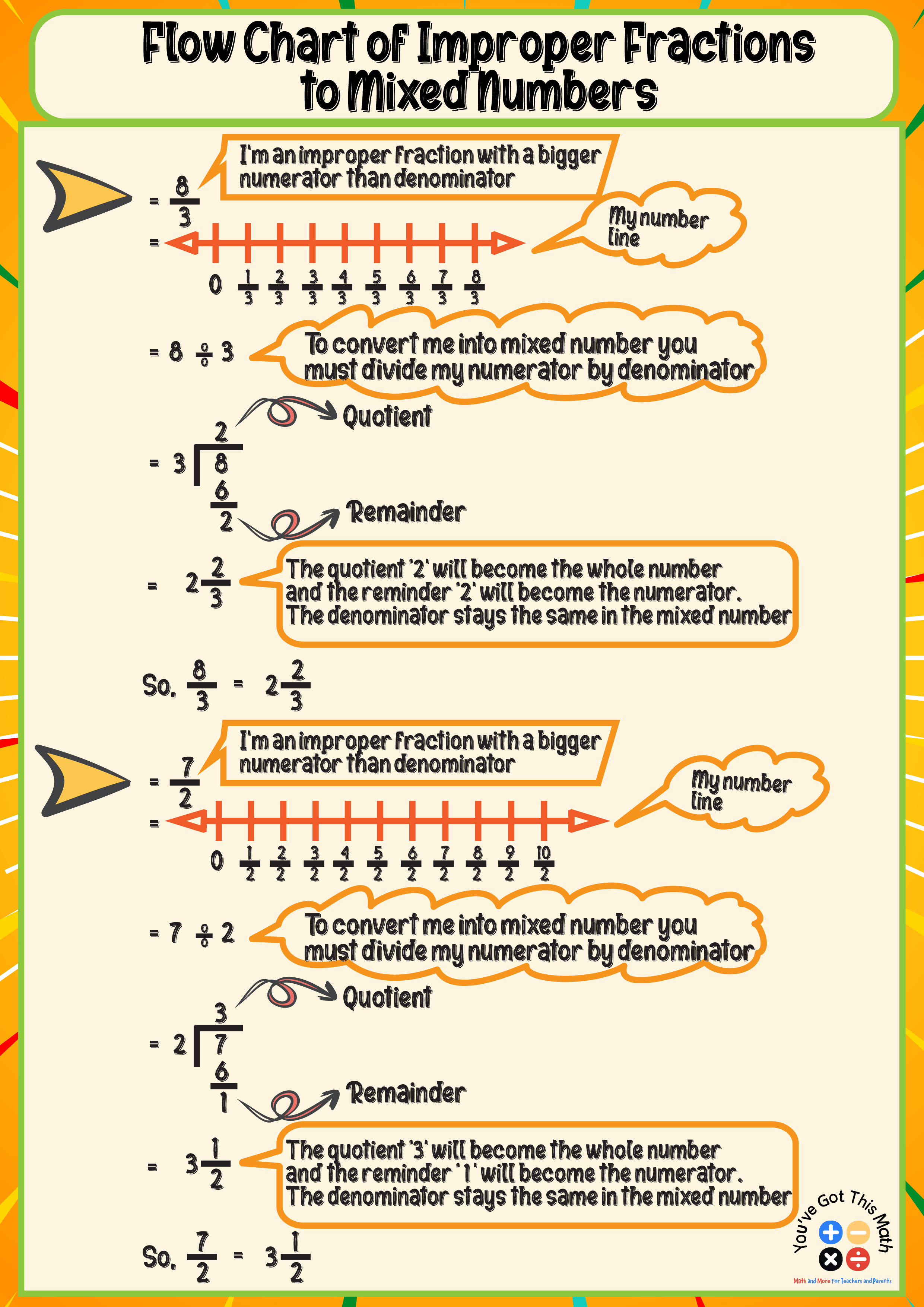
Improper Fraction to Mixed Numbers on a Number Line
In this method, the students draw the number line of the given improper fraction, such as 8/3, where the numerator 8 is bigger than the denominator 3. They draw the number line of 8/3 and mark that as an improper fraction.
Then, they divide the numerator 8 by the denominator 3, and the quotient 2 acts as the whole number, and the remainder 2 acts as the numerator. The denominator (3) remains the same. They also simplify the mixed number if needed.
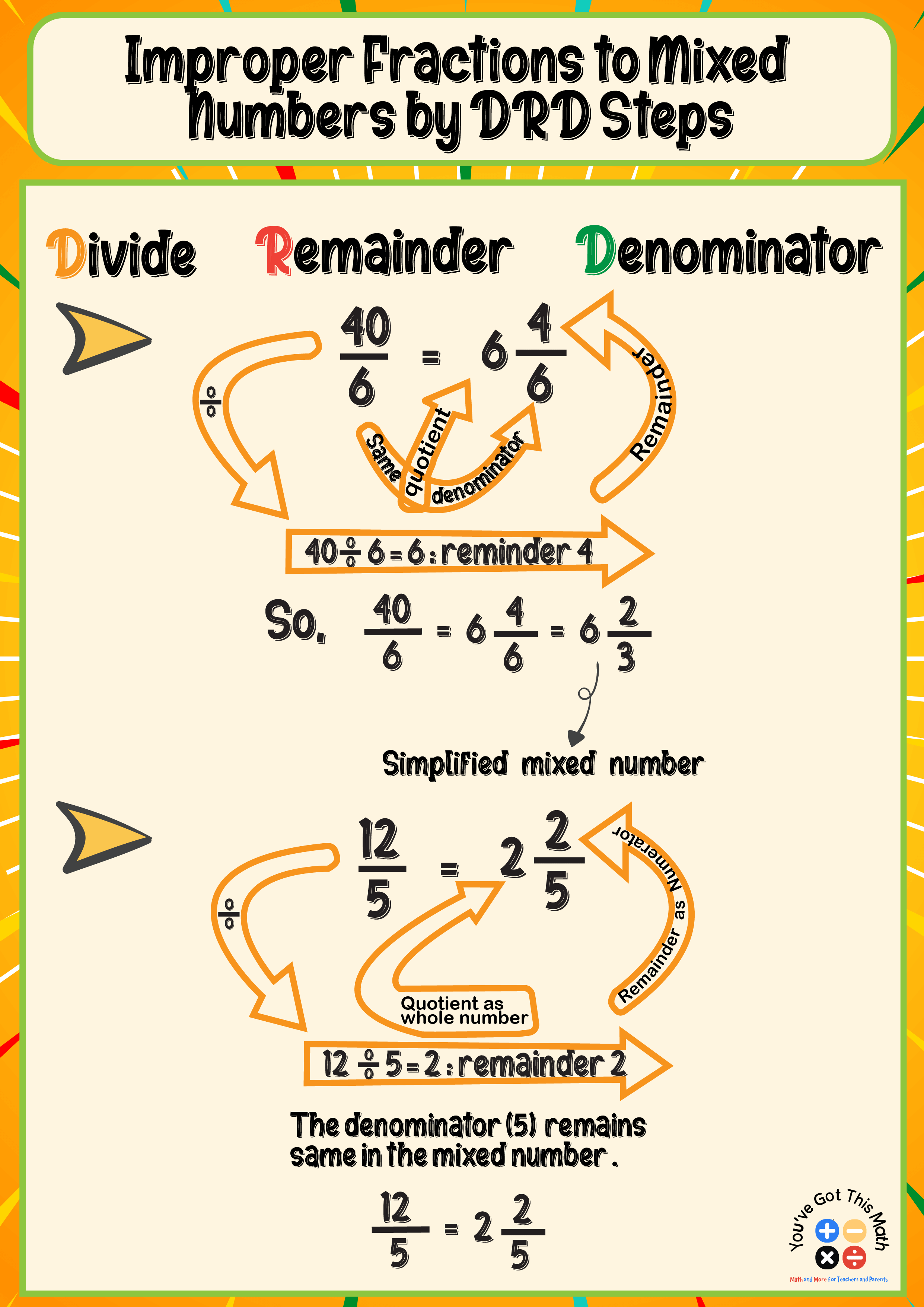
Improper Fractions to Mixed Numbers by DRD (Divide, Reminder, Denominator)
Converting improper fractions to mixed numbers follows the DRD steps. The steps are given below:
Step 1: Divide the numerator by the denominator, such as 40/6 is an improper fraction. Divide the numerator 40 by the numerator 6.
Step 2: The quotient of the division will be the whole number, which is 6, and the remainder will be the new numerator of the mixed number, which is 4.
Step 3: The denominator 6 remains the same. Simplify the fraction if needed.
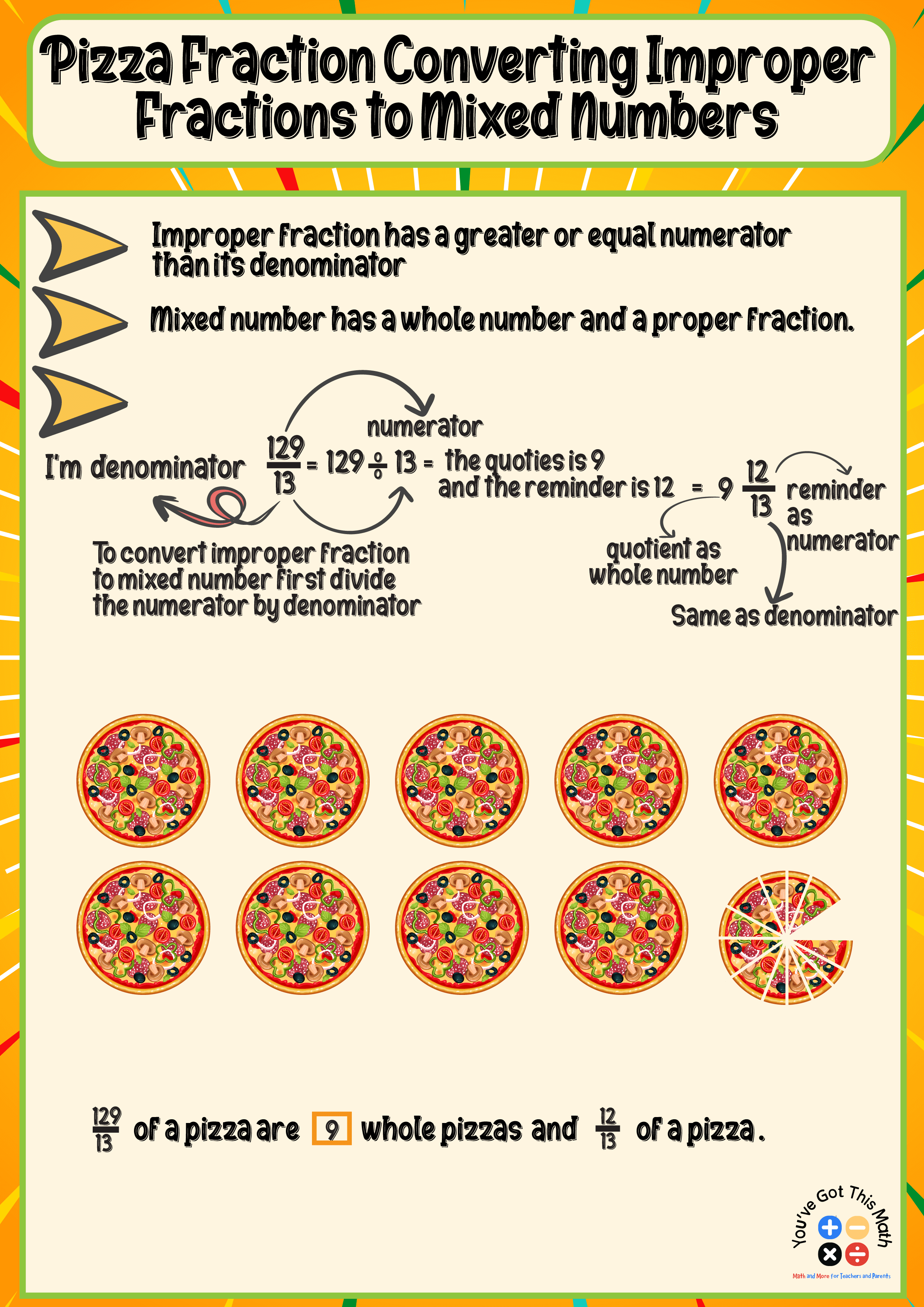
Converting Improper Fraction to Mixed Numbers Using Pizza Models
Children easily understand converting an improper fraction to a mixed number through a practical example like pizza.
If you look at the improper fraction 129/13, it might not be easy to visualize the number that it represents since the numerator is greater than the denominator. To convert this, the first thing you need to do is divide the numerator of the fraction by the denominator. The quotient 9 will be the whole number, and the remainder 12 will be the numerator. The denominator stays the same.
Download Free Worksheet PDF
Download the following combined PDF and enjoy your practice session.
So today, we’ve discussed improper fractions to mixed numbers anchor chart with examples using the concepts of proper fractions, improper fractions, mixed numbers, etc. Download our free worksheets, and after practicing these worksheets, students will surely improve their mathematical skills and have a better understanding of fraction.