Comparing Fractions Anchor Chart | 9 Fun Examples
These comparing fractions anchor chart examples will help to visualize and understand comparing fractions. 4th and 5th-grade students will learn basic fraction methods and can improve their basic math skills with our free printable comparing fractions anchor chart.
9 Exciting Examples of Comparing Fractions Anchor Chart
Please download the following comparing fractions anchor chart and practice examples on the pages.
Comparing Fractions with the Help of Common Numerator
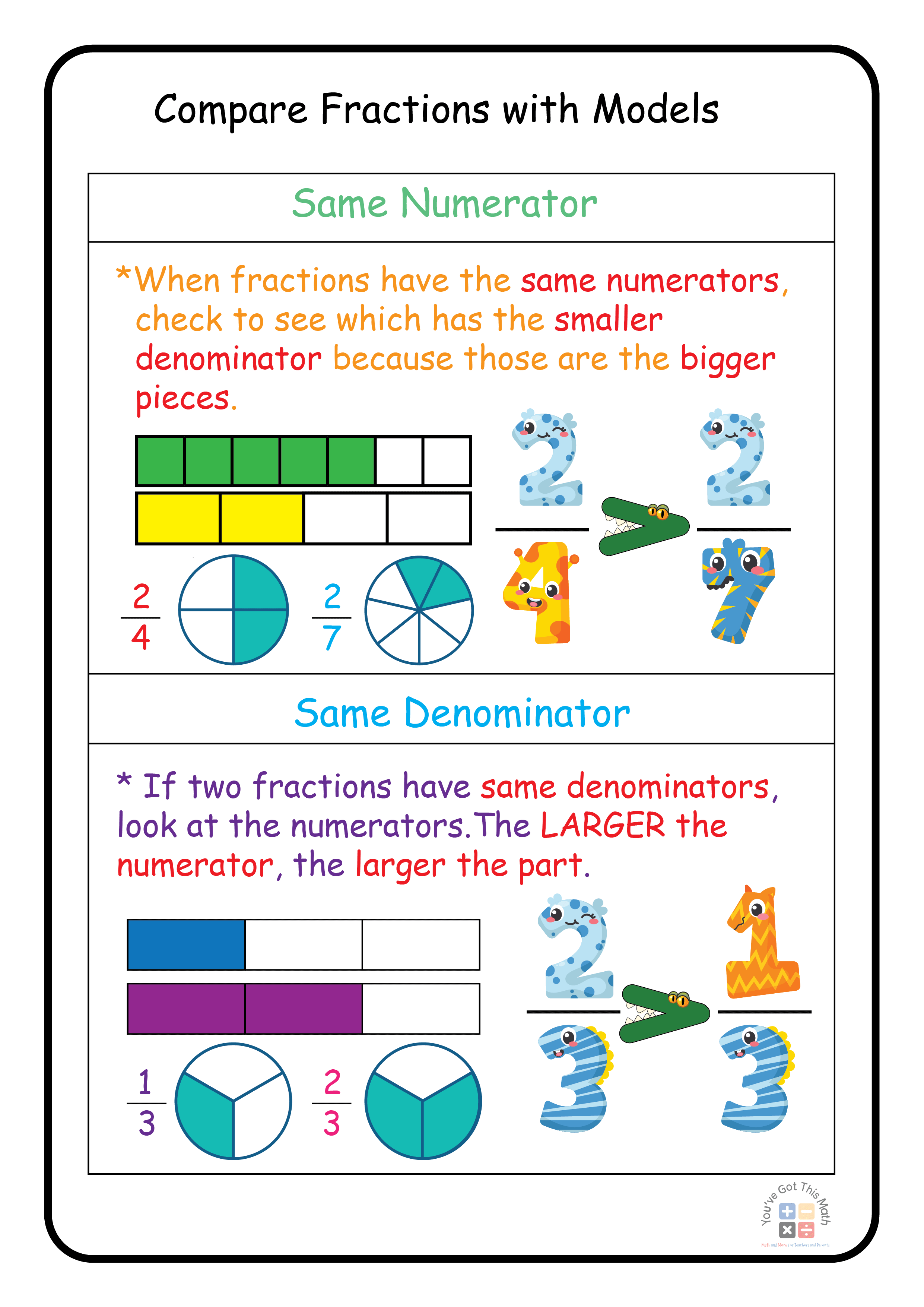
Compare the denominators of fractions with the common numerator to compare them. The fraction whose denominator is larger is smaller.
On the other hand, the fraction will be larger if the denominator is smaller.
Comparing Fractions with the Help of the Same Denominator
It is simpler to identify the larger or smaller fraction when comparing fractions with the same denominator. We may easily find the fraction with the larger numerator by first determining whether the denominators are the same.
The fractions are equal if the numerators and denominators are both equal. Let’s compare 6/17 with 16/17 as an illustration.
Step 1: Check the fractions’ denominators (6/17 and 16/17). The numerators are identical.
Step 2: Compare the numerators now. It is clear that 16 > 6. Step 3: The greater fraction is the one with the larger numerator. Consequently, 6/17 < 16/17.
Fractions Comparing with Unlike Denominator
We can simply compare the fractions when the denominators are the same. Let’s compare 1/2 and 2/5 as an example.
Step 1: Check the fractions’ denominators, which are 1/2 and 2/5. They are different. Thus, let’s calculate the LCM of 2 and 5. LCM(2, 5) = 10.
Step 2: Let’s now convert them so that their denominators are the same. Let’s multiply the first fraction by 5/5, which is 5/10 when multiplied by 1/2.
Step 3: Let’s now multiply the second fraction by 2/2, which equals 2/5 x 2/2 = 4/10.
Step 4: Compare the fractions 5/10 and 4/10 in step 4. We will compare the numerators because the denominators are the same, and we can see that 5 > 4 by doing so.
Step 5: The greater fraction, 5/10 > 4/10, is the fraction with the larger numerator. Consequently, 1/2 > 2/5.
It should be remembered that we can simply compare fractions by looking at their denominators if the denominators are different and the numerators are the same.
The fraction that has a smaller denominator is worth more, whereas the fraction that has a larger denominator is worth less. 2/3 > 2/6, for instance.
Fractions Comparing with Unlike Numerator
This method is similar to the previous method.
The Least Common Multiple (LCM) of the denominators should be determined in order to transform fractions with unlike numerators into fractions with similar denominators for comparison.
We can simply compare the fractions when the denominators are the same. Let’s compare 3/5 and 4/10 as an example.
Step 1: Check the fractions’ denominators, which are 3/5 and 4/10. They are different. Thus, let’s calculate the LCM of 5 and 10. LCM(5,10) = 10.
Step 2: Let’s now convert them so that their denominators are the same. Let’s multiply the first fraction by 2/2, which is 6/10 when multiplied by 3/5.
Step 3: Let’s now multiply the second fraction by 1/1, which equals 4/10 x 1/1 = 4/10.
Step 4: Compare the fractions 6/10 and 4/10 in step 4.
We will compare the numerators because the denominators are the same, and we can see that 6 > 4 by doing so.
Step 5: The greater fraction, 6/10 > 4/10, is the fraction with the larger numerator. Consequently, 3/5 > 4/10.
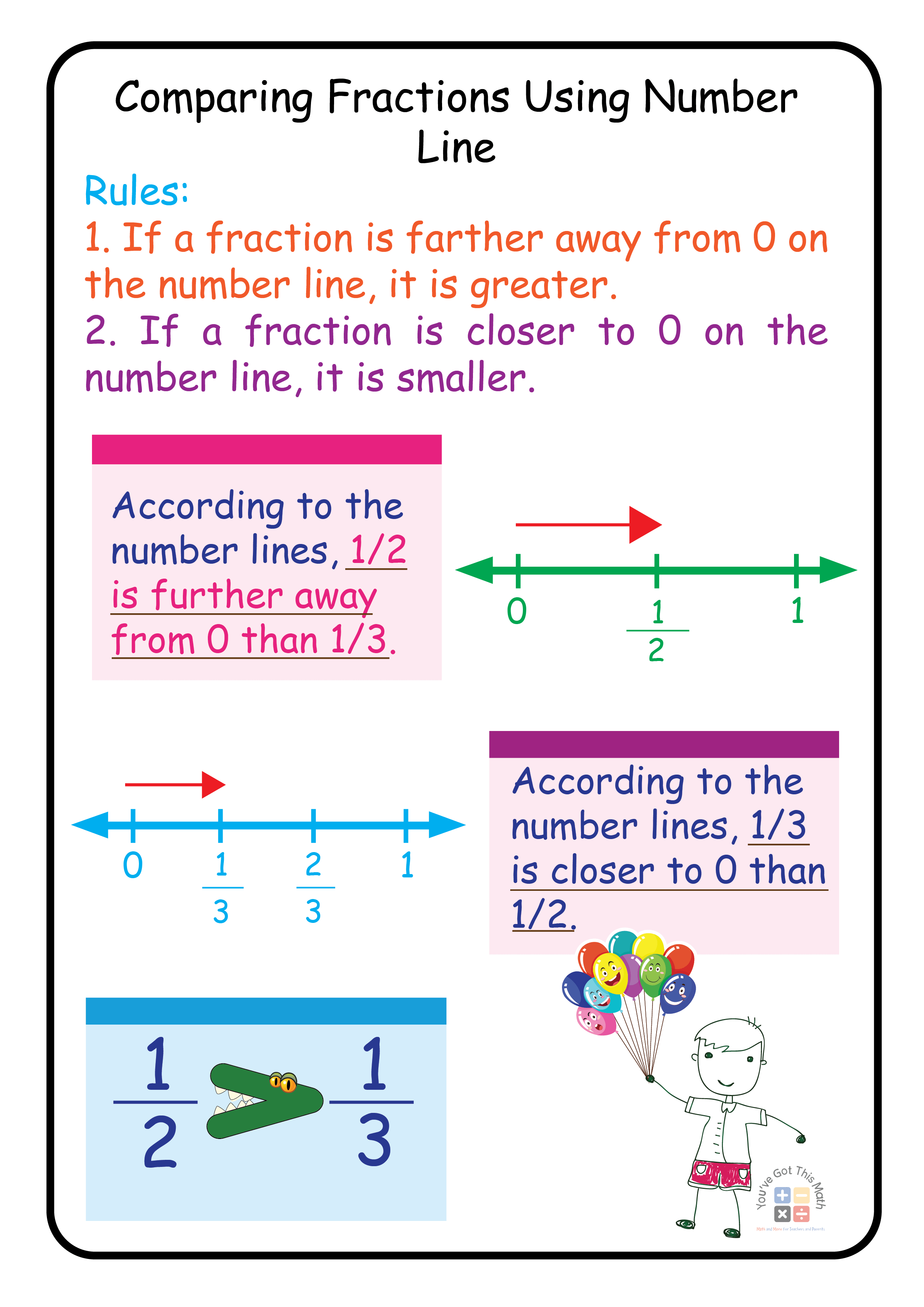
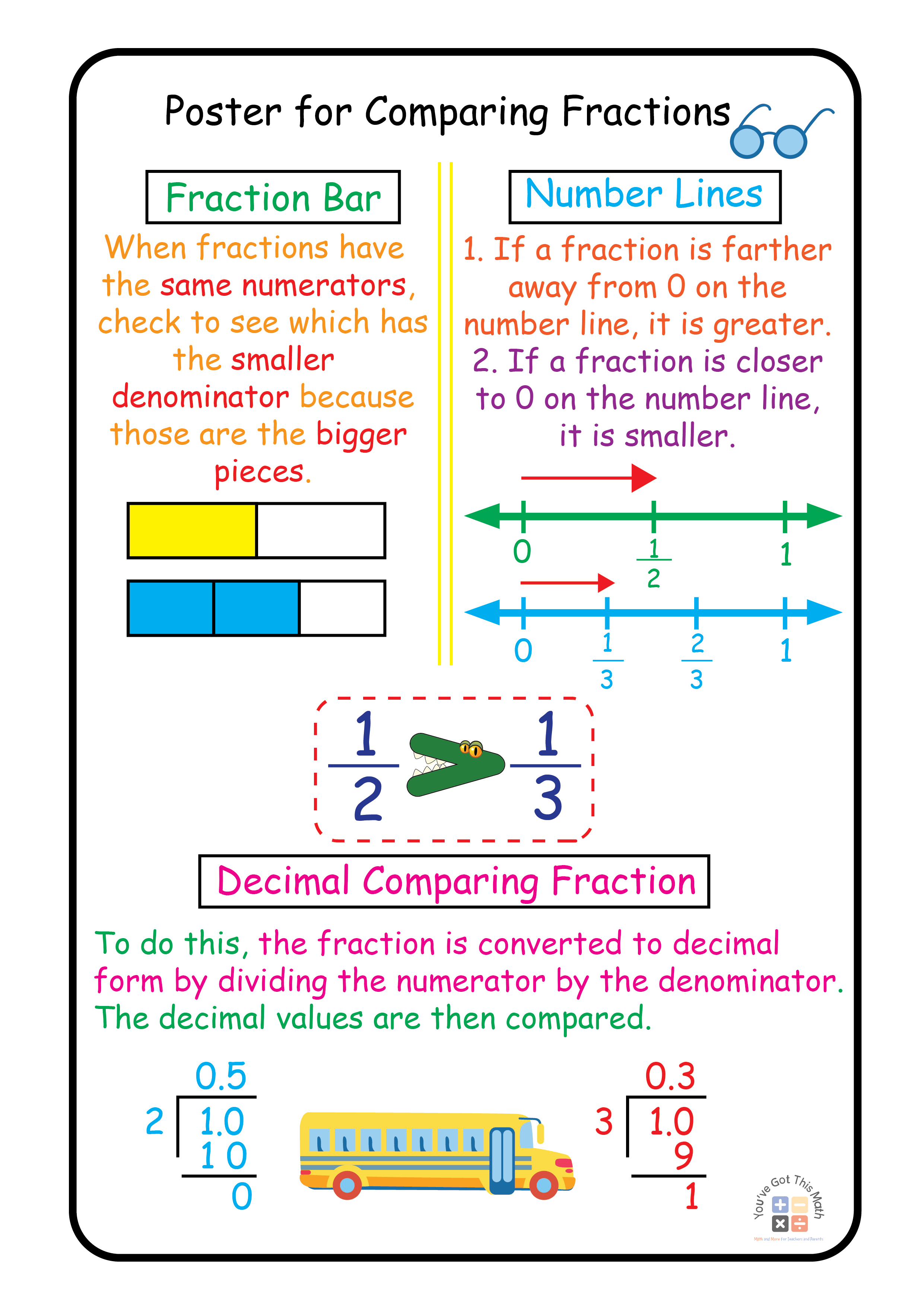
Comparing Fractions Using Number Line
If a fraction is farther away from 0 on the number line, it is greater. If a fraction is closer to 0 on the number line, it is smaller.
Let’s take a look at an illustration. These represent the halves and thirds on the number line. According to the number lines, 1/2 is further away from 0 than 1/3. Accordingly, 1/2 is greater than 1/3.
Compare Fractions Using Models
In this chart, students will learn how to compare fractions with the help of area models.
Fractions Comparing Using Butterfly Method
This method is similar to the cross-multiplication method. We multiply the numerator of one fraction by the denominator of the second fraction to compare fractions using cross multiplication.
Let’s use an illustration to better grasp this.
Compared to 3/4 and 1/2, See the illustration below for a clearer explanation of this.
Step 1: When cross-multiplying the given fractions for comparison, keep in mind that the product should be written next to the original fraction if the first fraction’s numerator is being multiplied by the second fraction’s denominator.
We will put 4 next to the first fraction, as 1 x 4 equals 4. (Put the product on the selected numerator’s side.)
Step 2: Write the result next to the second fraction when multiplying the numerator of the second fraction by the denominator of the first fraction. In this case, 3 x 2 equals 6, so we will put 6 close to the second fraction.
Step 3: Now compare products 4 and 6. Since 4 <6, it is simple to compare the corresponding fractions, which are 1/2 <3/4. Consequently, 1/2< 3/4.
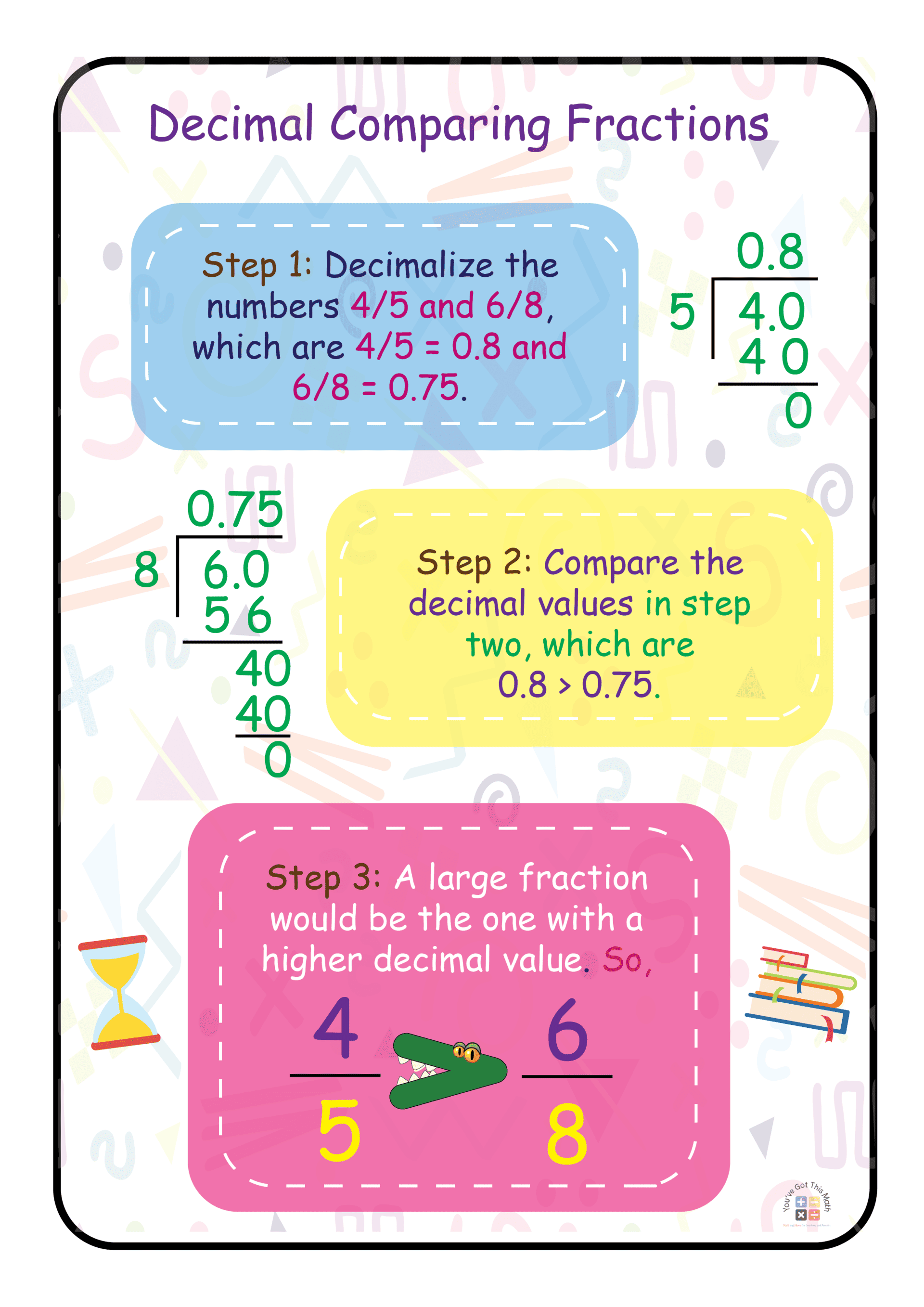
Comparing Fractions with the Help of Decimals
This approach compares fractional and decimal numbers. To do this, the fraction is converted to decimal form by dividing the numerator by the denominator.
The decimal values are then compared. Let’s compare 4/5 and 6/8 as an example.
Step 1: Decimalized the numbers 4/5 and 6/8, which are 4/5 = 0.8 and 6/8 = 0.75.
Step 2: Comparing the decimal values in step two, which are 0.8 > 0.75. Step 3: A larger fraction would be the one with a higher decimal value. So, 4/5 is larger than 6/8.
Fractions Comparing with Bar Models
This posters help students compare fractions.
Download Free Worksheet PDF
Download the following combined PDF and enjoy your practice session.
So today, we’ve discussed comparing fractions anchor chart examples using the concepts of common and unlike denominator, like and unlike numerator, butterfly method, models, and number line. Download our free worksheets, and after practicing these worksheets, students will surely improve their mathematical skills and have a better understanding of fraction.

Hello!
Welcome to my profile. I have done my graduation from Ahsanullah University Of Science and Technology in Electrical and Electronic Engineering. Currently, I have started working as a Content Developer for “You’ve got this math” at SOFTEKO. As an Electric engineer, I always try to achieve innovative knowledge. I have an interest in research articles on different ideas. Also, I really like to solve innovative and mathematical problems. I really hope I’ll do better in the future as an Engineer.