Adding Fractions with Unlike Denominators Anchor Chart | Free Printable
These adding fractions with unlike denominators anchor chart will help to visualize and understand fractions and arts of the fractions. 3rd and 4th-grade students will learn basic subtraction methods and can improve their basic math skills with our free printable adding fractions with unlike denominators anchor chart.
6 Free Adding Fractions with Unlike Denominators Anchor Chart
With the aid of these worksheets, our kids will be able to master fundamental mathematics quickly and actively. Download the following worksheets and practice.
Visual aids called anchor charts are frequently utilized in educational contexts, especially in classrooms. Teachers and students work together to produce these big, vibrant posters, which are intended to aid pupils in remembering key ideas and facts.

Fractions: Definition and Fraction Vocabularies
A fraction in mathematics is a portion of a whole or a ratio of two numbers. The numerator and denominator are written one number above the other, separated by a horizontal line. Like other numbers, fractions can be added, subtracted, multiplied, and divided using a variety of mathematical operations.
The main two parts of a fraction are the numerator and the denominator. The numerator and denominator of a fraction are the numbers above and below the fraction line, respectively.
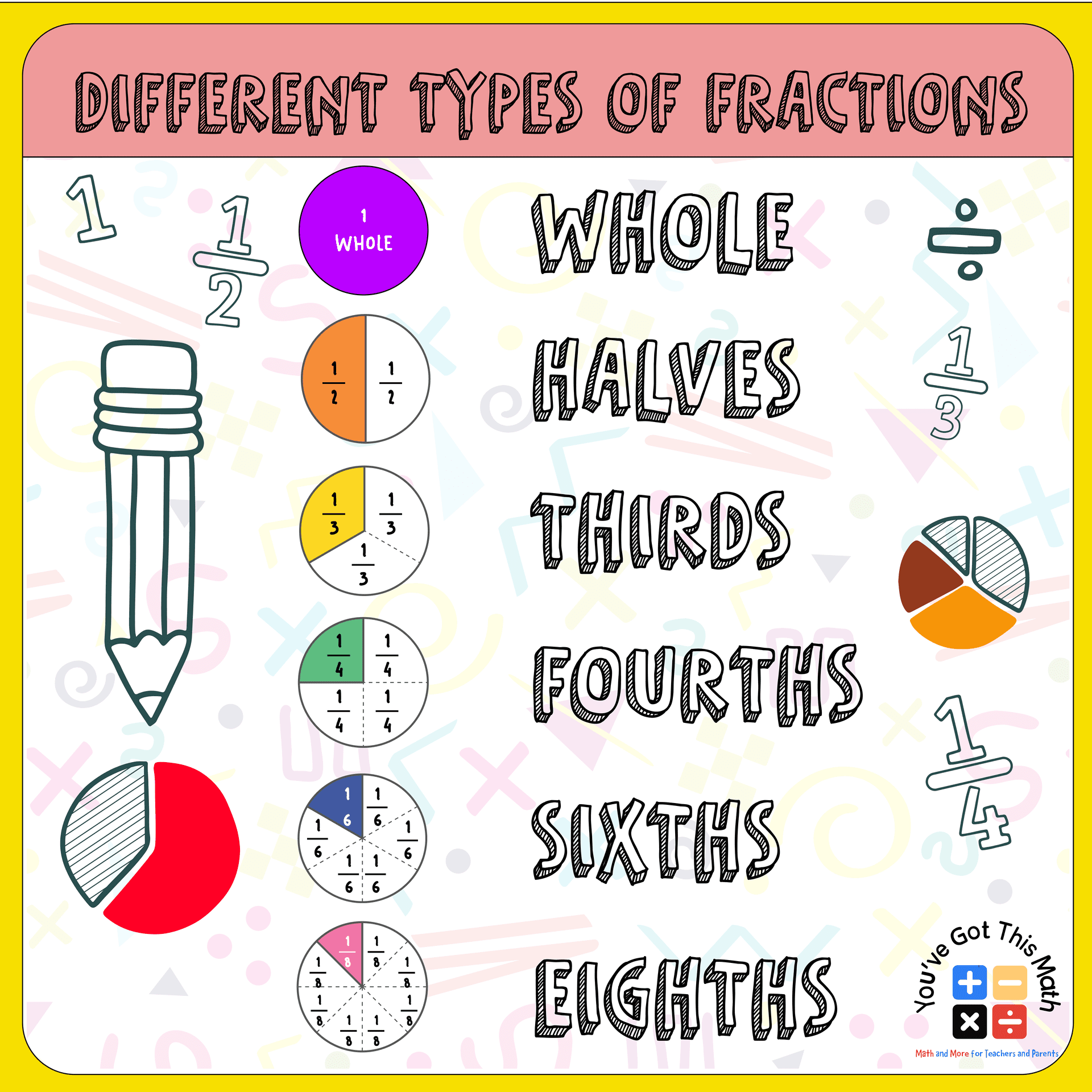
How to Create an Addition of Fractions with Unlike Denominators Anchor Chart
An anchor chart is a visual representation of a topic that makes the topic easily representable to the students in a classroom. In this article, we target on adding fractions with unlike denominators anchor chart to show the steps of the operation.

Step, Details, and Elements of a Good Fraction Anchor Chart
When creating a fraction anchor chart, it is important to follow the following steps and use the elements.
Step 1: Choose a title that accurately reflects the content of the anchor chart.
Step 2: Introduce the concept of fractions and define key terms.
Step 3: Include visual representations of fractions such as pie charts, number lines, or fraction bars.
Step 4: Provide examples of how to compare fractions using visual models and common denominators.
Step 5: Include examples of adding and subtracting fractions with common and different denominators.
Step 6: Provide examples of multiplying and dividing fractions and explain how to simplify fractions.
Step 7: Include practice problems that reinforce the concepts covered in the anchor chart.
Step 8: Summarize the key concepts covered in the anchor chart.
4 Interesting Examples to Add Fractions with Unlike Denominators Anchor Chart
This article will provide you with 4 interesting examples of adding fractions with unlike denominators anchor chart. This is an effective procedure to teach children basic mathematical operations using anchor charts. Follow the examples one by one and you will get a clear idea about anchor charts to add fractions.
Common Denominator Method to Add Fractions with Unlike Denominators Anchor Chart
This example is quite interesting. Follow the step-by-step procedure given below.
Steps:
- First, extract the denominators from the fractions:
- Then find the Least Common Multiples (LCM) of them.
- After that, find the equivalent fraction of those two fractions. The denominators will be the same as the LCM.
- Add the Fractions then.

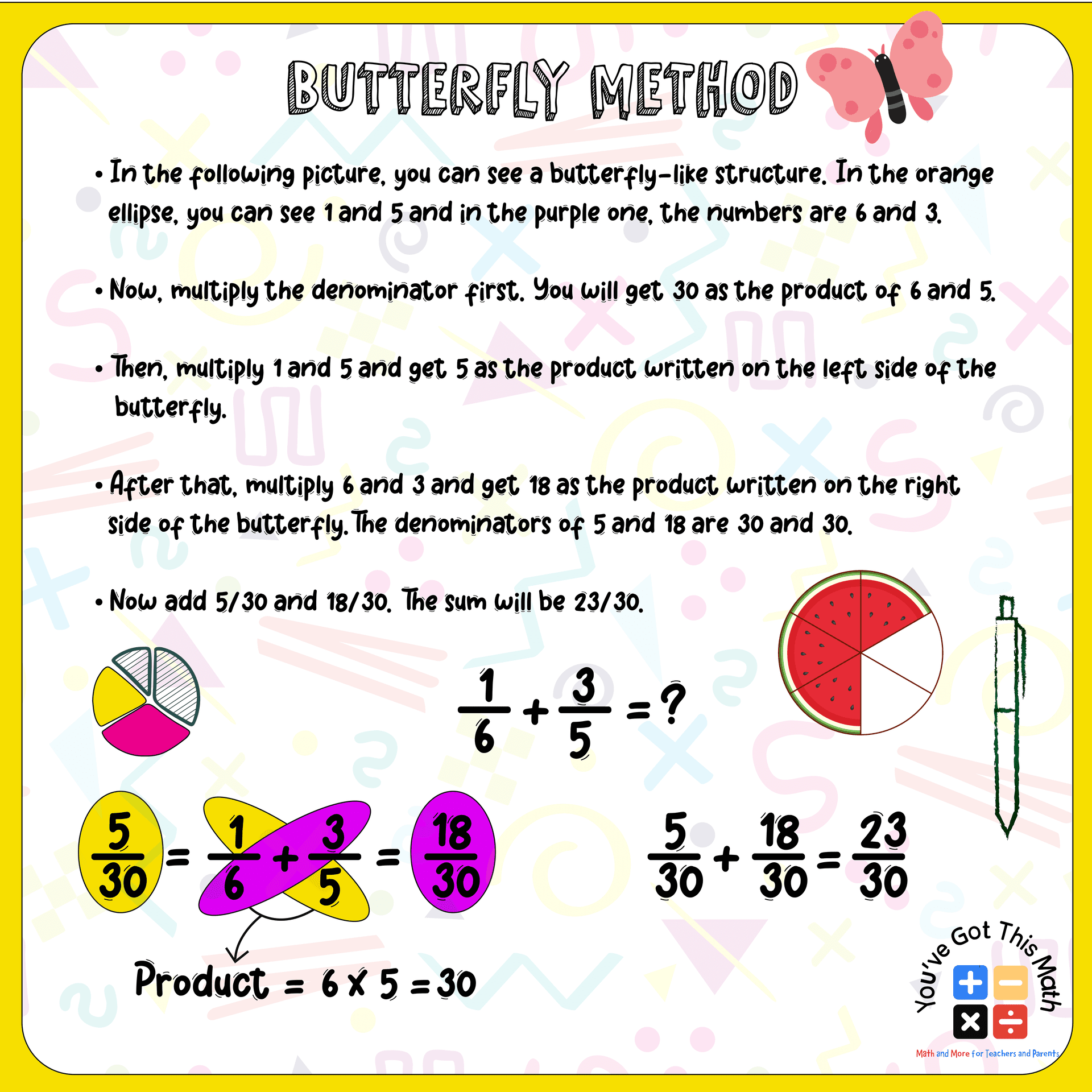
Butterfly Method to Add Fractions with Unlike Denominators Anchor Chart
This is an easy method. I am going to show an example here. Simply follow the steps shown in the example.
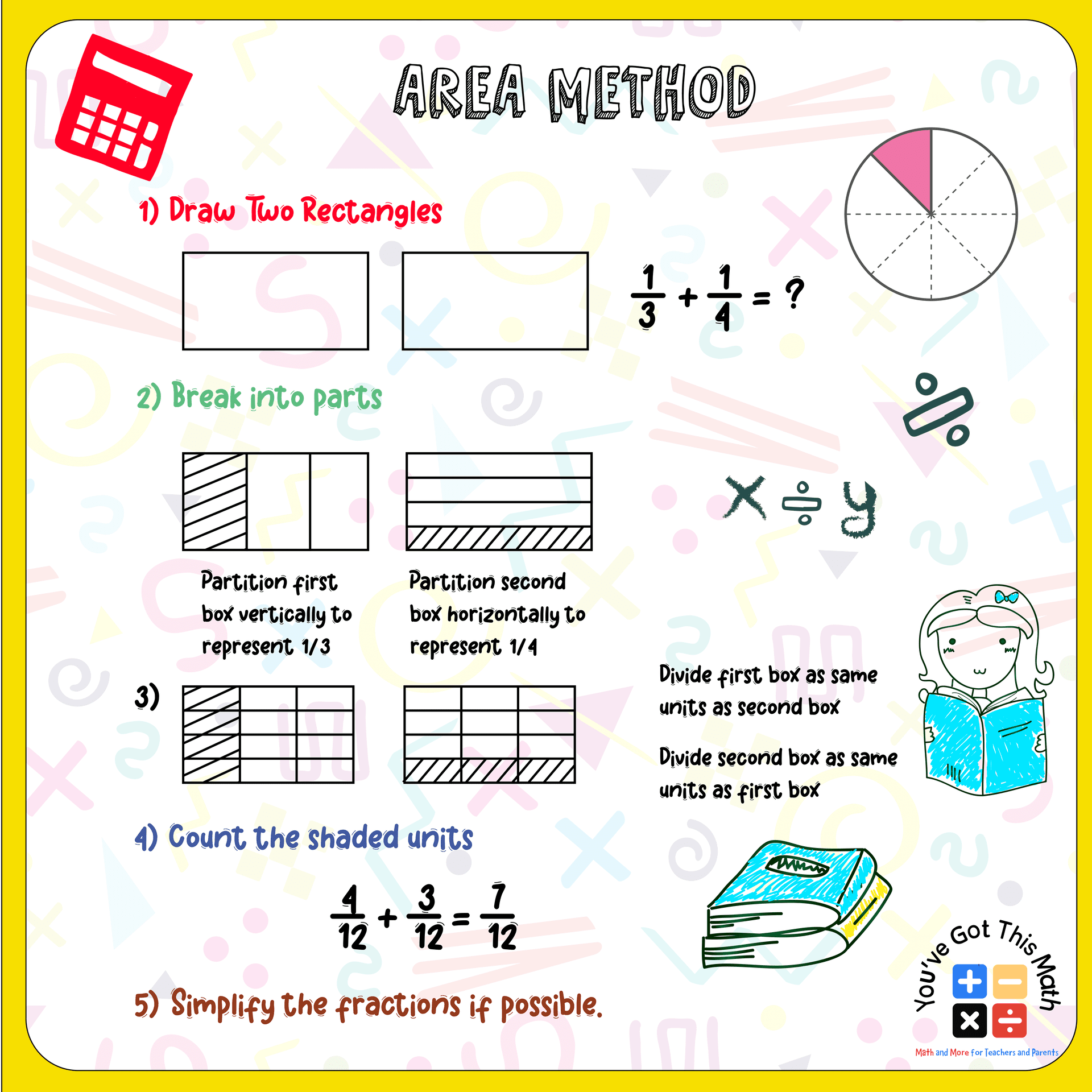
Adding Fractions with Unlike Denominators Anchor Chart Using Area Method
This is also a funny and colorful method. Follow the steps of the example.
Adding Fractions with Unlike Denominators Using Equivalent Fraction
Here, I will find the equivalent fraction first from the LCM and then make a summation of the fractions with unlike denominators.

Adding Fractions with Like & Unlike Denominators Anchor Chart
Follow the steps of the solutions in the following example.
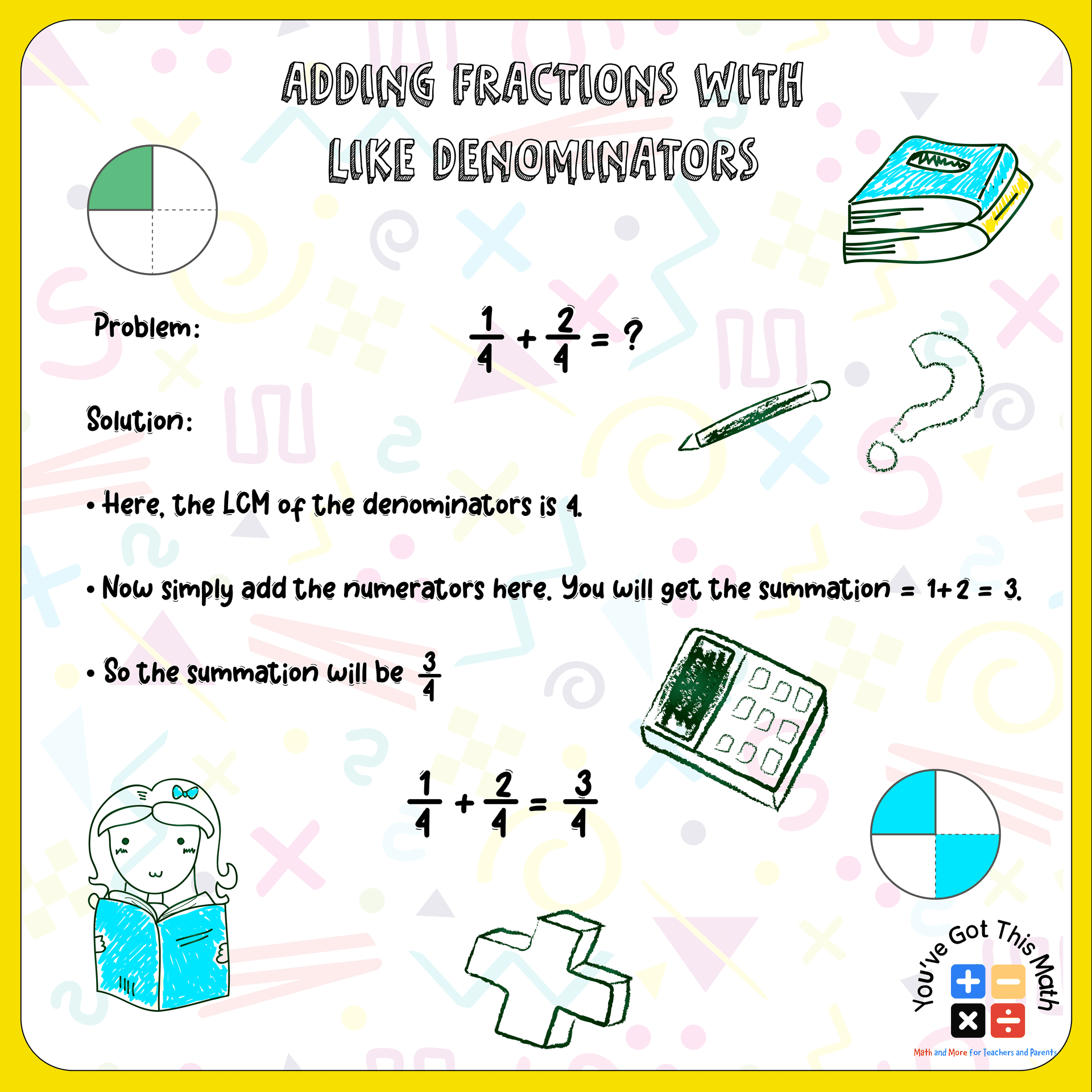
Adding and Subtracting Fraction with Unlike Denominators Anchor Chart
Here I am going to show a new anchor chart to make a solution of subtracting fractions with unlike denominators. Follow the following solution to the problem.

Download the Free PDF
Download the following free worksheet PDF and print out the anchor chart for your students.
So today, we’ve discussed adding fractions with unlike denominators anchor chart using the concepts of common denominator method, butterfly method, area method, and equivalent fraction method. Download our free worksheets, and after Practicing these worksheets, students will surely improve their mathematical skills and have a better understanding of the addition of fractions.

Hi there! This is Souptik Roy, a graduate of the Bangladesh University of Engineering and Technology, working as a Content Developer for the You Have Got This Math project of SOFTEKO. I am a person with a curious and creative mind. After finishing my Engineering degree, I want to explore different fields. This is why I am working here as a content developer. I have a massive interest in creative content writing. When I find that someone can learn something from my articles, this gives a lot of inspiration. hopefully, you will find interest in my article, if you have a child and want to teach them math with fun.







