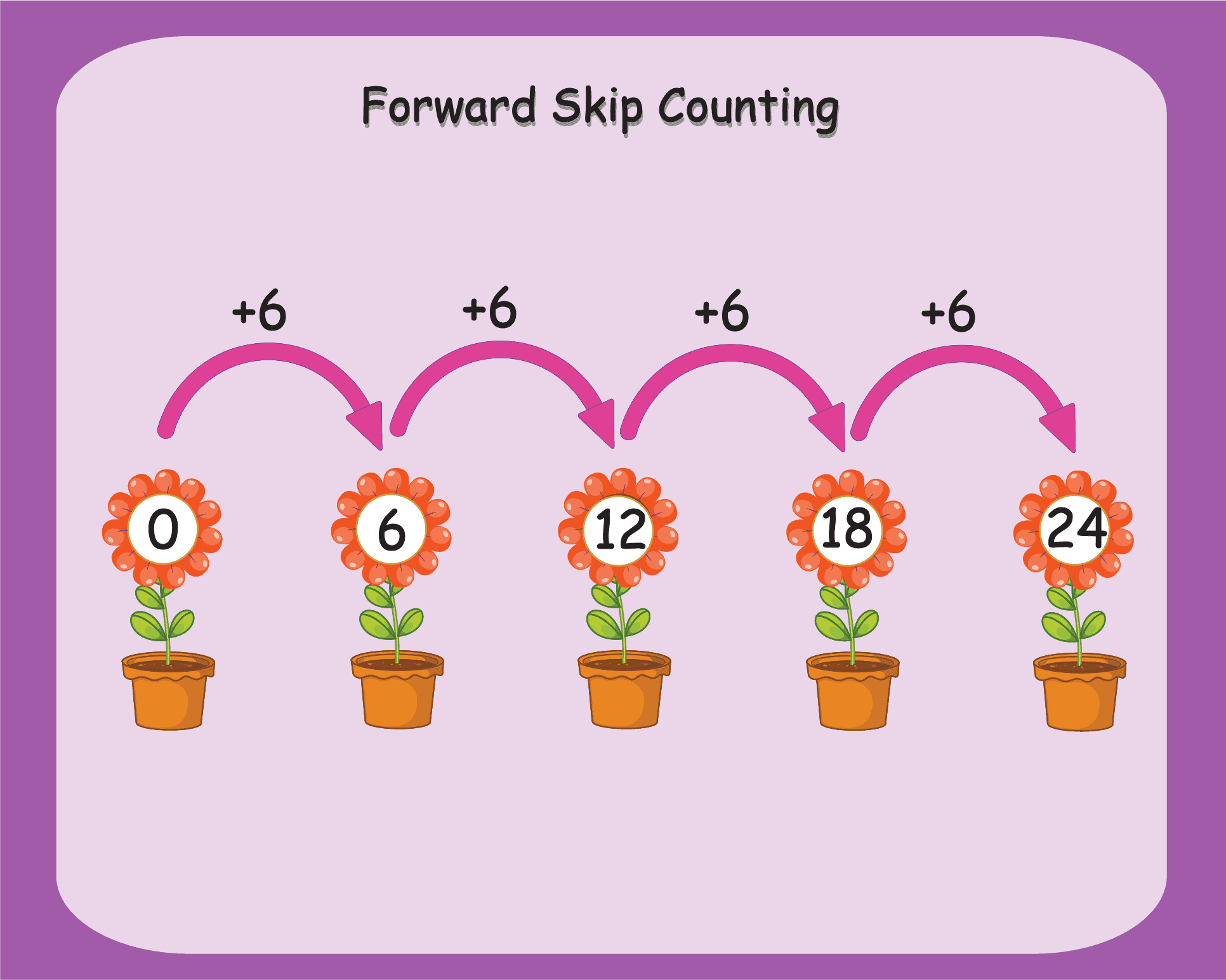Skip Counting on a Number Line | 11 Free Worksheets
Buy 2700+ Pages Math Games & Activities (PreK-2nd Grade)
These worksheets on skip counting on a number line will help to visualize and understand skip counting and number recognition systems. 5th-grade students will learn basic skip counting methods and can improve their basic math skills with our free printable skip counting on a number line worksheets.
11 Exciting Skip Counting on a Number Line Worksheets
Please download the following skip counting on a number line worksheets and practice skip counting problems on the pages.

Definition of Skip Counting
Skip counting is the process of counting by repeatedly adding the same number.
One can skip count by any number other than 1, though the most common skip counts are 2, 3, and 10. It involves repeatedly adding the same amount because the count is based on repeated addition.
When we count by skipping one number and immediately moving on to the next, we are said to be “skip counting.” On the number line, skip counting can be used forward and backward.
As an example, if we were to skip count by 2, starting at 0, the next number would be 0 + 2 = 2, then, 2 + 2 = 4, then 4 + 2 = 6, then 6 + 2 = 8, and then, 10, 12, 14, 16, 18, and so on.
Forward Skip Counting
We only skip positive numbers when counting forward. The number series moves ahead in this case because we must add a specific number to the previous number.
The image contains a problem of forward skip counting by 6.
Backward Skip Counting
Negative integers are used to skip numbers when counting backward. In this situation, the sequence of numbers moves backward as we subtract one number from the previous number.
An example of backward skip counting by 7 is shown here.
Skip Counting on a Number Line by 2
A step-by-step way of adding or removing the number 2 is to skip count by 2.
This will produce a series of different even numbers. In a number line, we are skipping over twos here. So, starting at 10, the next number will be 10 + 2 = 12, then 12 + 2 = 14, then 14 + 2 = 16, then 16 + 2 = 18, and then 20, 22, 24, 26, 28, and so on.
Backward and Forward Skip Counting by 2 on a Number Line
We only skip positive numbers when counting forward. The number series moves ahead in this case because we must add a specific number to the previous number.
Negative integers are used to skip numbers when counting backward. As we reduce one number from the previous number, the series of numbers moves backward in this case.
Skip Counting by 2 on a 100s Chart
Let’s look at the chart below, which shows skip counting by 2. A pattern was observed as we proceeded and skipped a number.
As we skip count by 2, the numbers in the chart below go from 2 to 4, 6, 8, and so on. Starting with 0, we add 2 to the previous number to produce the following number. When skip counting by 2, the graph below reveals the vertical patterns.
Skip Counting on a Number Line by 3
Look at a number line when doing skip counting by three. Beginning with 0, we move on to the third number, 3, after skipping the first two.
We again skip two numbers and move right to the third number after 3, which is 6, to get to the following number by counting by three. Next, we move on to 9 and then to 12, and so on, continuing in the same way. Hence, the list created by skipping three digits is 0, 3, 6, 9, and 12.
Skip Counting Backward and Forward by 3 on a Number Line
Forward skip counting by 3 involves adding three to each number to get the next one in the series. When forward skip counting by three, the list that results looks like 0, 3, 6, 9, 12, and so on.
As an alternative, backward skip counting by 3 involves counting backward and removing three from each number to get the next one in the sequence. Beginning with 99, the sequence produced by backward skip counting by three looks like 99, 96, 03, 90, 87, and so on.
Skip Counting by 3 on a 100s Chart
Let’s highlight the results of this method in the table of numbers below now that we have learned how to skip count by 3. Three is the first number. We highlight the numbers 6, 9, 12, 15, and so on as we skip count by three.
The numbers obtained by skipping counting by three form a diagonal pattern, as shown in the graph below.
Skip Counting on a Number Line by 4s and 8s
When we skip counting natural numbers by 4 and 8, we add 4 and 8 at each step. For example, starting at 10, the next number will be 10 + 4 = 14, then 14 + 4 = 18, then 18 + 4 = 22, and then 26, 30, and so on. Again, starting at 10, the next number will be 10 + 8 = 18, then 18 + 8 = 26, then 26 + 8 = 34, and then 42, 50, and so on.
Skip Counting on a Number Line by 5s and 10s
To count every fifth number starting with the given number, skip count by 5.
Beginning at zero, we count 0, 5, 10, 15, 20, 25, etc. On the other hand, a skip count of 10 means counting every tenth number starting from the given number. If we start at 0, we count 0, 10, 20, 30, etc.
Fun Skip Counting by 100 on a Number Line
Let the little number hoppers skip count in 100s and fill in the boxes as they hop down the number line. The key to completing the number line PDFs is to note how the number in the hundreds place increases by one each time.
Skip Counting on a Number Line Maze Challenge
Various entertaining mazes with various themes and scenarios can be found in this pdf. Solve them according to the instructions.
Download Practice Worksheets PDF
Download the following combined PDF and enjoy your practice session.
So today, we’ve discussed some skip counting on a number line worksheets using the concepts of skip counting by 2s, 4s, 5s, 8s, etc. Download our free worksheets, and after Practicing these worksheets, students will surely improve their mathematical skills and have a better understanding of skip counting on number lines.

Hello!
Welcome to my profile. I have done my graduation from Ahsanullah University Of Science and Technology in Electrical and Electronic Engineering. Currently, I have started working as a Content Developer for “You’ve got this math” at SOFTEKO. As an Electric engineer, I always try to achieve innovative knowledge. I have an interest in research articles on different ideas. Also, I really like to solve innovative and mathematical problems. I really hope I’ll do better in the future as an Engineer.