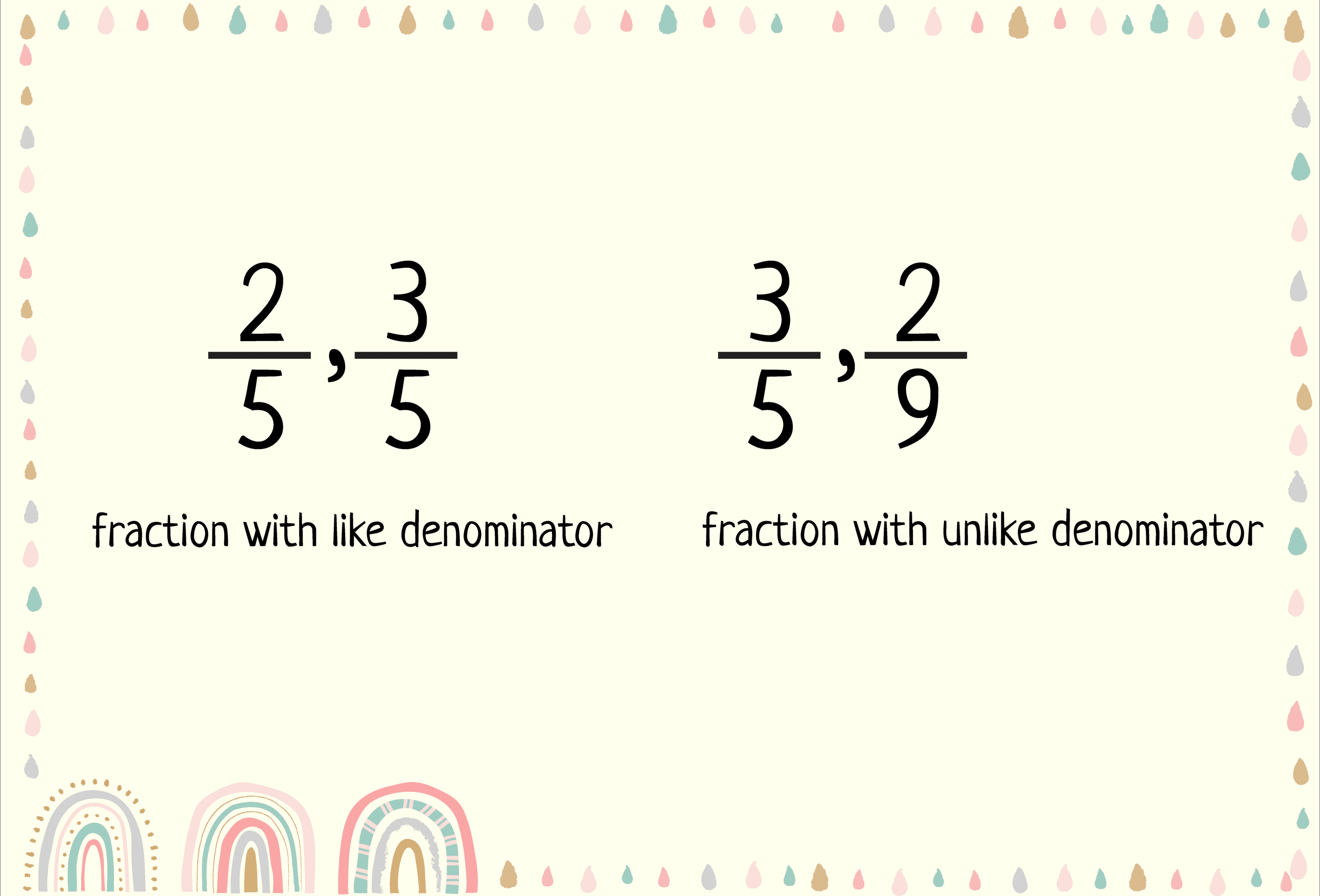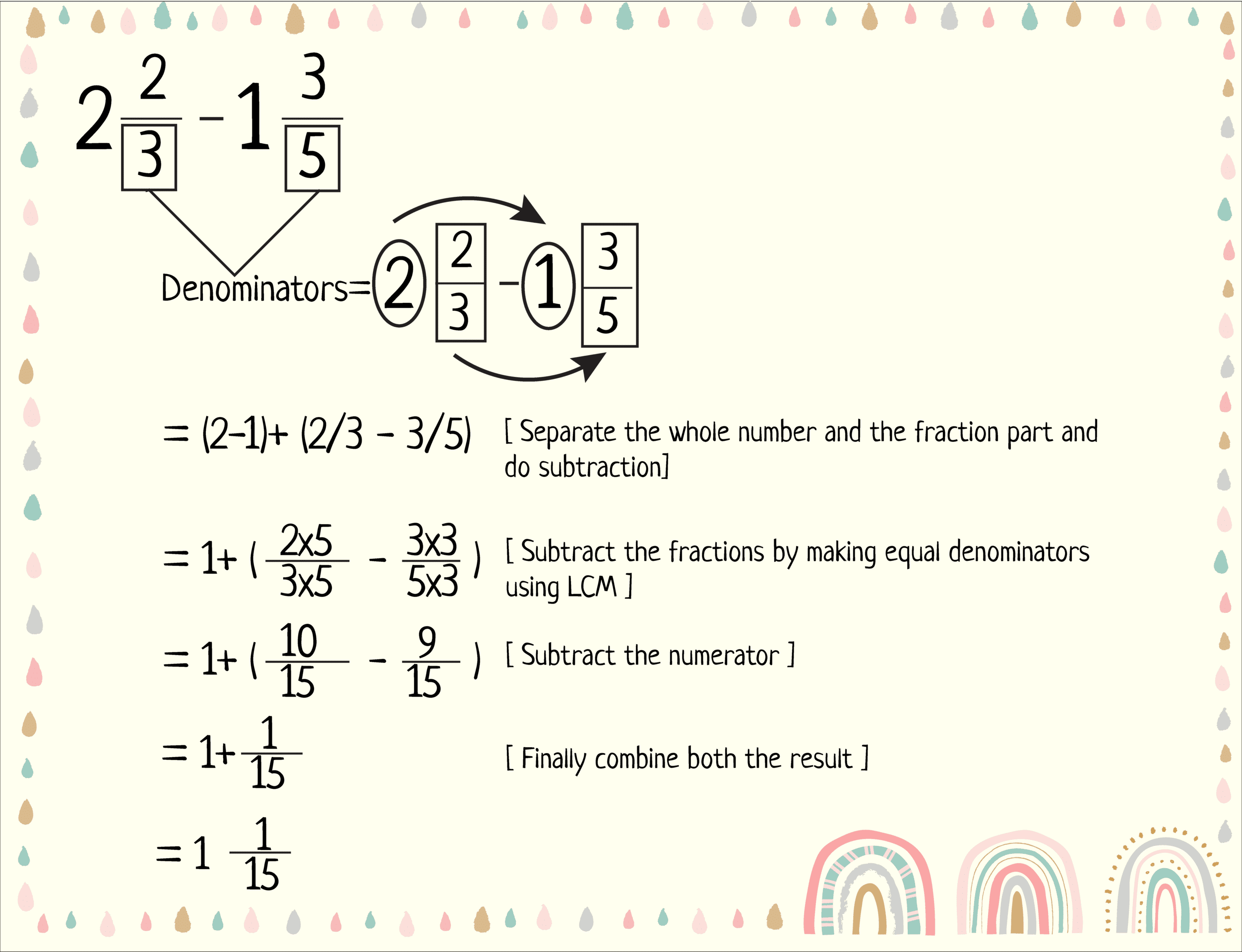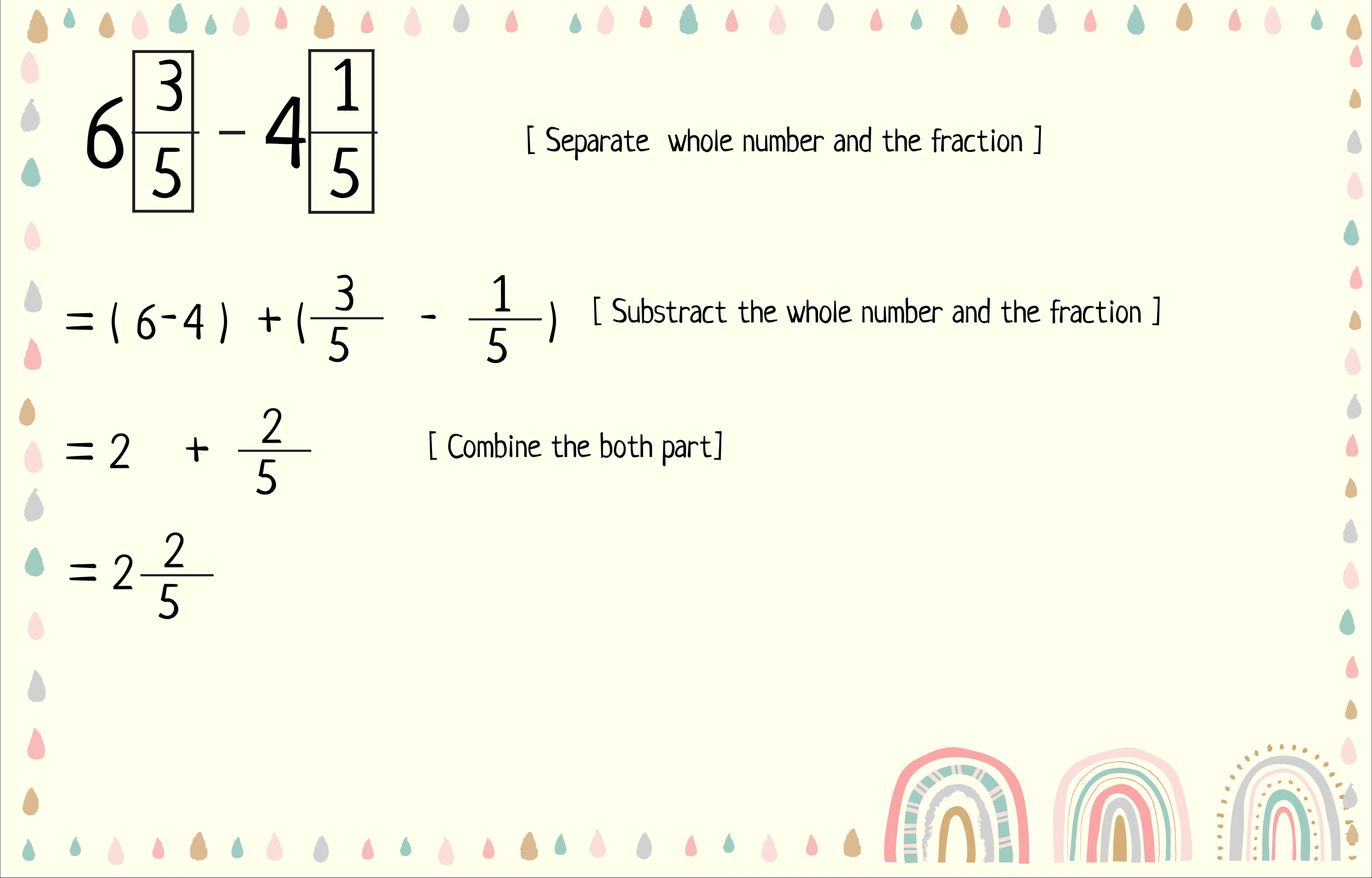6 Free Subtracting Mixed Fractions with Unlike Denominators Worksheets
These subtracting mixed fractions with unlike denominators worksheets will help to visualize and understand subtracting mixed fractions and number system. 5th-grade students will learn basic operations like subtraction of mixed fractions with unlike denominators and can improve their basic math skills with our free printable subtracting mixed fractions worksheets.
6 Exciting Subtracting Mixed Fractions with Unlike Denominators Worksheets
Please download the following subtraction worksheets and practice subtractions of mixed fractions on the pages.
What Are Mixed Fractions?
Fractions are different from integers. When a number is not whole or complete, we express it as a fraction.
When we are talking about mixed numbers or fractions, the names of their components come first. Basically, a mixed number or fraction is formed by two things, a whole number and a proper fraction.
At this point, there may be a question inside you all. When is the term mixed numbers used? Or when do we need to work with mixed numbers?
A mixed number or mixed fraction is related to an improper fraction. When the denominator of a fraction is smaller than the numerator, it is called an improper fraction.
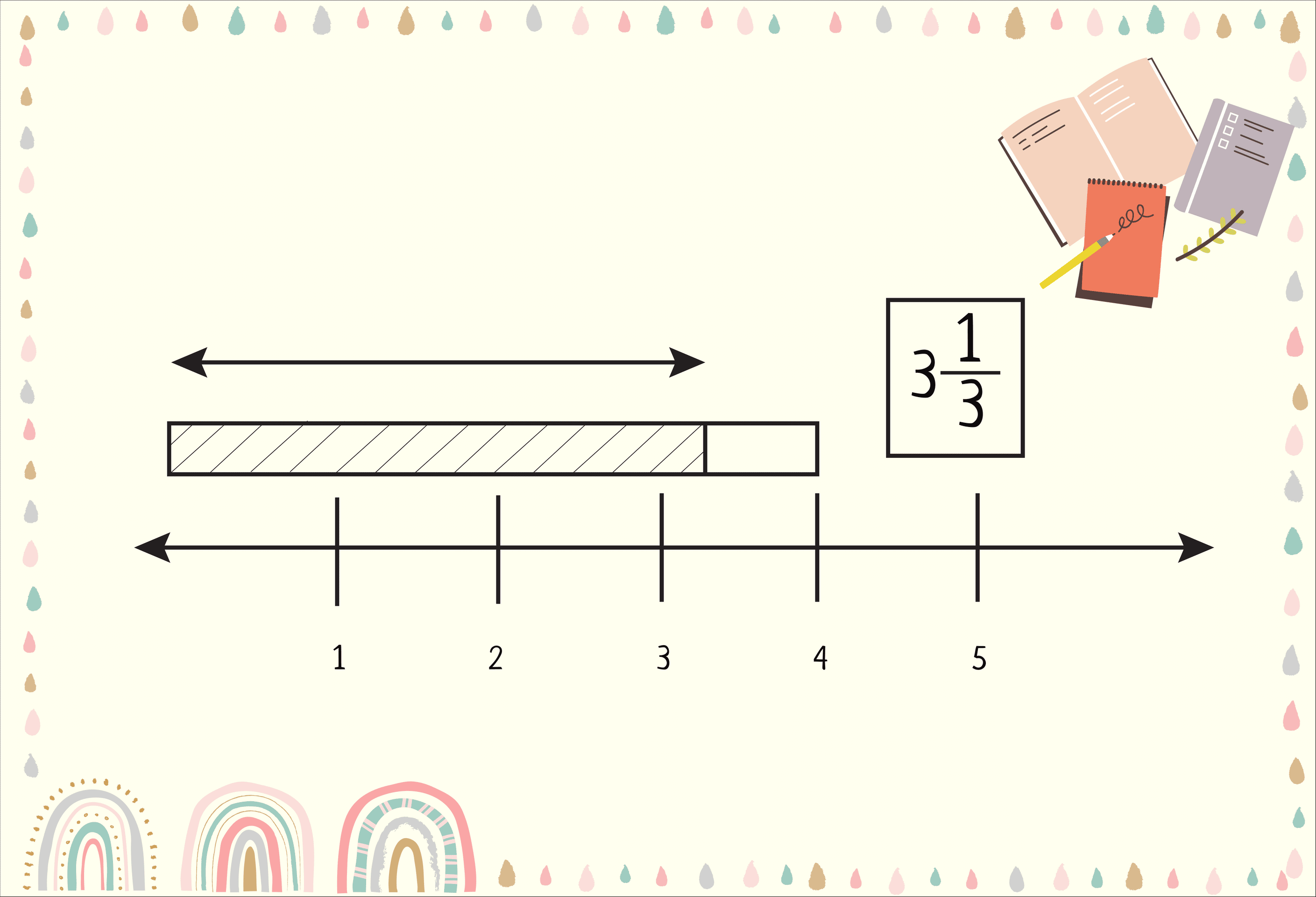
For example, Xavier has four homework assignments, each of which is three pages. If he finished 10 pages of homework, that means he had finished 3 homework and 1 page of the last one. To express it as a mixed fraction, we can write, that Xavier has finished 3 1/3 of his homework.
Let’s end this discussion after explaining one more topic. What are fractions with unlike or different denominators?
We know a fraction consists of a numerator and a denominator. When two denominators of two fractions are the same, then we call those fractions the same or like denominators.
For example, 2/7 and 5/7 are two fractions, and the denominators of both fractions are 7. So, we can tell that both of these fractions have the same or similar denominators.
Again, consider two fractions 3/5 and 2/9. Here, the denominators for both fractions are not the same, and they are 5 and 9, respectively. So, these types of fractions are called fractions with unlike denominators.
Some Real Life Examples of Subtracting Mixed Numbers
Before going on to the main discussion, let’s see some real-life examples of subtracting mixed numbers.
- If you are having 5 glasses of hot chocolate and your friends drink only 3 and 1/2 glasses from you, then you are left with 1 1/2 glasses of hot chocolate with you.
- If you have two watermelons and eat only 1/4 of the first melon, then you are left with 1 3/4 of the melon.
- If you are participating in a race on a 5-mile track and have finished running about 2 and a quarter miles, then you have more than 2 3/4 miles to cover.
3 Exciting Examples of Subtracting Mixed Fractions with Unlike Denominators
In the following discussion, you will find three exciting examples and methods of subtracting mixed fractions with unlike denominators. Understand each of the examples thoroughly to become a champion at subtracting mixed fractions with unlike denominators.
So, without any delay, let’s start our journey.
Subtracting Whole Numbers and Fractions Parts Separately
In the first method, we will subtract the whole number and the fraction part of two mixed numbers separately to complete our task. For that, we need to make the unlike denominators of the two fractions into like denominators. See the following steps for a better understanding.
- First, take both mixed fractions and identify their whole numbers and fraction parts.
- Separate the whole number and the fraction part of both fractions, like in the following image.
- Subtract the second fraction’s whole number from the first fraction and write the result.
- As the denominators of the fraction parts of both fractions are not the same, use the Least Common Multiple (LCM) method to do the subtraction.
- Then simplify the result if necessary, and lastly, combine the result of the subtraction of the whole part and the fraction part.
- See the final result of the subtraction after completing all the steps.
Now, to improve your skill on the above discussion, practice the following subtraction problem by applying the above-mentioned technique.
Subtracting Mixed Fractions with Unlike Denominators after Converting into Improper Fractions
In this method, we will subtract two mixed numbers, after converting them into improper fractions. How we do that is given in the following steps.
- First, take both mixed fractions and identify their whole numbers and fraction parts.
- Then convert the mixed fractions to improper fractions.
- For that, multiply the whole numbers by the denominators of the fractions and add the multiplication results to the numerators of the fractions.
- Use the least common multiple to make both denominators equal.
- As both the denominators are now equal, simply subtract the numerator.
- Simplify the result, if necessary, and turn the improper fraction into a mixed number.
- To do that, divide the numerator of the improper fraction by its denominator.
- You will find the quotient as a whole number part, and the remainder of that division becomes the numerator of the proper fraction, while the denominator remains as it was before.
Now, to improve your skill on the above discussion, practice the following subtraction problem by applying the above-mentioned technique.
Subtracting Mixed Fractions with Unlike Denominators Using Regrouping
In all the above examples, you can see that the fraction parts of the larger mixed fractions were always bigger than the fraction parts of the smaller mixed fractions. That’s why you can subtract those mixed numbers using the above two methods.
But when the scenario changes, meaning if the fraction part of the larger mixed fraction is smaller than the smaller mixed fraction’s fraction part, then you can take advantage of regrouping. See the following steps for more details.
- First, take both mixed fractions and identify their whole numbers and fraction parts.
- As the denominators of both fractions are not the same, you have to use the least common multiple to find a common denominator for both fractions.
- As the numerator of the first fraction is smaller than the second one, we cannot directly subtract them.
- So, to subtract and make the first numerator bigger, we have to borrow from the whole number of the first mixed fraction that is on the left side of the fraction part.
- We need to add the borrowed part in fractional form.
- In our example, we borrow 1 from the whole number 8. Now, we can write 1 as 6/6 which is a fractional form, and both the denominators are equal.
- As we borrowed 1 from the whole number 8, we are now going to write 7 instead of 8.
- Now, regroup 6/6 with 2/6, that gives you 8/6.
- Afterward, as shown in Example 1, subtract the whole numbers and the fraction parts separately.
- Then simplify the result if necessary, and lastly, combine the result of the subtraction of the whole part and the fraction part.
- See the final result of the subtraction after completing all the steps.
Now, to improve your skill on the above discussion, practice the following subtraction problem by applying the above-mentioned technique.
Subtracting Mixed Fractions with Like Denominators
In the above discussion, you have seen examples of subtracting mixed fractions with unlike denominators. Let’s finish today’s lesson by showing you the steps to subtract mixed fractions with like denominators.
- Take two mixed fractions with the same denominator.
- Then subtract the whole number and the fraction part separately, as shown in the steps of Example 1.
- After that, combine the result of those two subtractions and do any simplification as needed.
- Get the final result of the subtraction after doing all the steps.
Now, to improve your skill on the above discussion, practice the following subtraction problem by applying the above-mentioned technique.
Download Free Printable PDF
Download the following combined PDF and enjoy your practice session.
So today, we’ve discussed subtracting mixed fractions with unlike denominators worksheets using the concepts of fractions, proper and improper fractions, mixed fractions, numerator and denominator, subtraction, and regrouping. Download our free worksheets, and after practicing these worksheets, students will surely improve their mathematical skills and have a better understanding of the subtraction of mixed fractions with unlike denominators.
Hello, I am Md. Araf Bin Jayed. I have completed my B.Sc in Industrial and Production Engineering from Ahsanullah University of Science and Technology. Currently I am working as a Content Developer for You Have Got This Math at Softeko. With proper guidelines and aid from the parent organization Softeko, I want to represent typical math problems with easy solutions. With my acquired knowledge and hard work, I want to contribute to the overall growth of this organization.