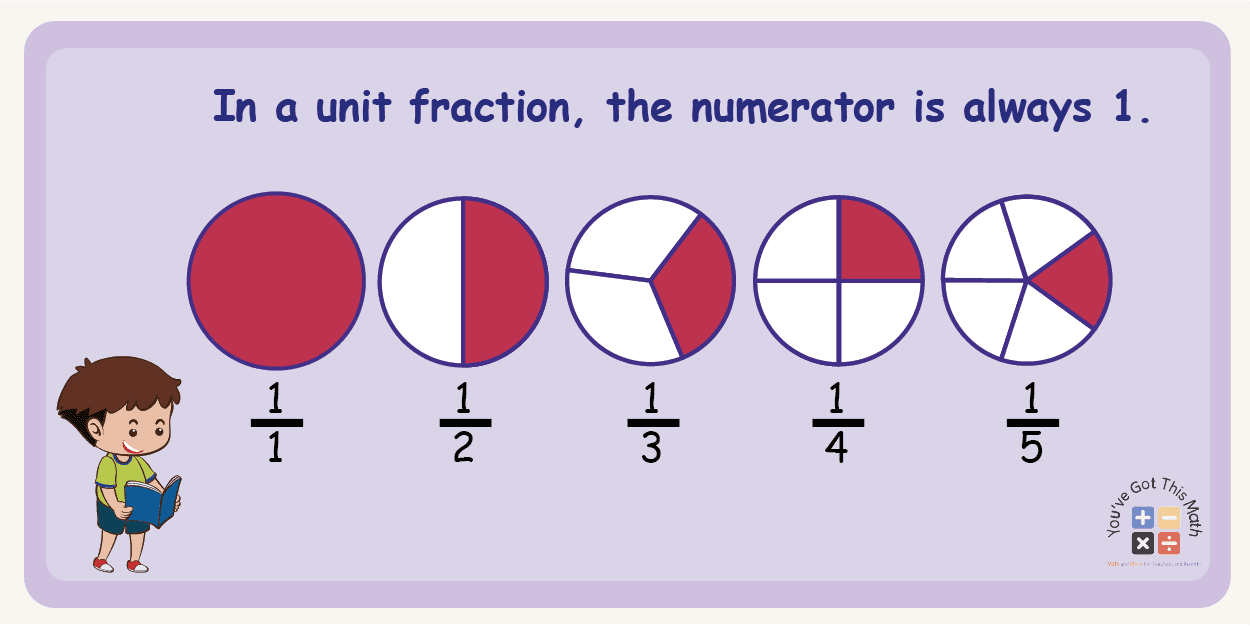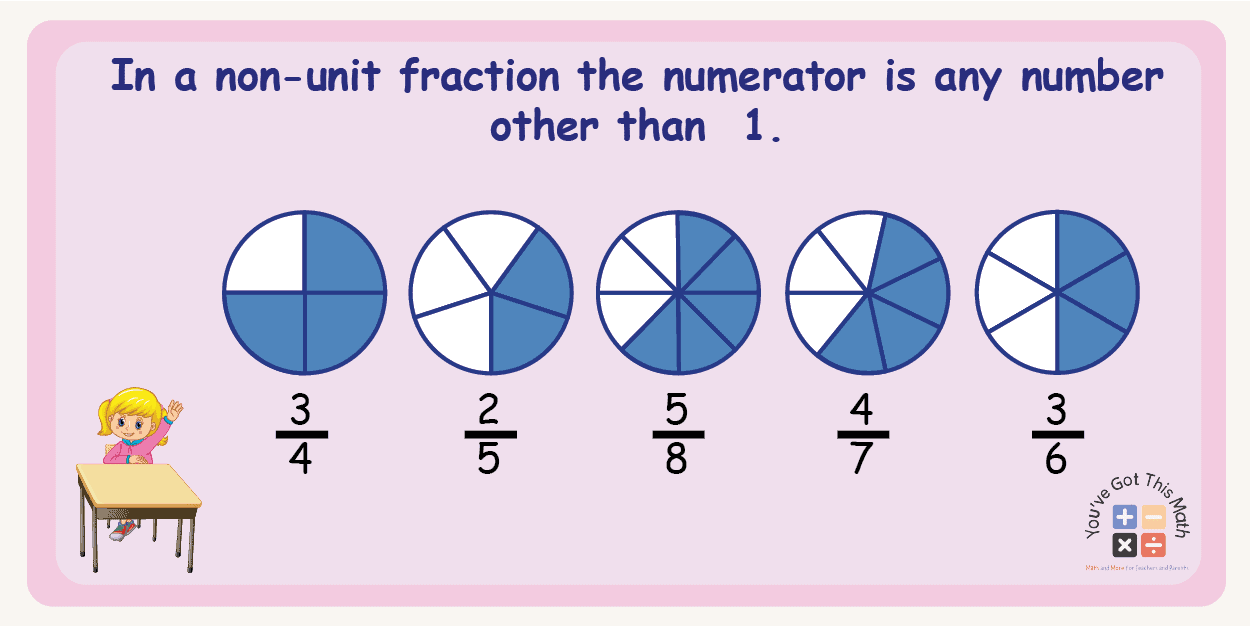What is Numerator and Denominator with Example | Free Worksheets
It’s impossible to have expertise in math without knowledge of division and fractions. As, we have to represent many values or figures in fractions. So, it’s an important question for youngsters what is numerator and denominator with example.
First things first. What do we have in fractions? Or how is a fraction made? Sounds interesting, right?
When we see a fraction, we can see two numbers separated by a horizontal line. They are called the numerator and denominator. Will the above two be the heroes of today’s lesson? Here we will learn what is numerator and denominator with example.
How are they related? Let’s find out.
Introduction to Numerator and Denominator of a Fraction
What is division? You have to consider two things for division. The dividend and the divisor. The number that we want to divide is called a dividend. And the number with which we want to divide is called a divisor.
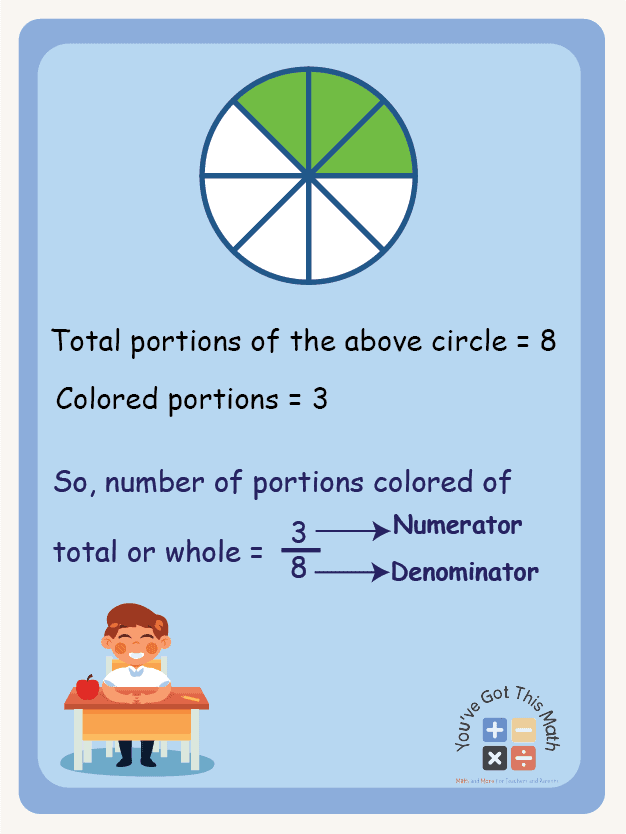
Now, when the results of a division don’t come as a whole or full number, they come as a fraction, like in the following image.
Look at the following circle. It’s divided into 8 equal pieces. Among the pieces, how many are colored?
Start to count. 1, 2, 3. Stop. Three Pieces, right?
So, among the 8 pieces, 3 are colored. This means about 3/8 of the circle is colored.
In the above discussion, where are the numerator and denominator?
The upper part of the fraction is called the numerator. It stands for the number of equal portions we take into consideration from a given quantity.
A fraction’s denominator, on the other hand, is its lower part. It represents the number of equally sized pieces into which an entire quantity is divided.
In the following example, the relationship between 3 and 8 can be represented as a fraction. And that will be 3/8. This means three portions of the total eight portions are colored.
So, here, 3 is acting as the numerator, and 8 is acting as the denominator.
Importance of Learning About Numerator and Denominator
You might wonder why it is important to learn about numerator and denominator and how these two terms will help us. First of all, think about what a numerator and denominator are related to.
Any ideas?
Yes. A fraction. Both of these things are related to fractions. So, understanding the numerator and denominator along with their relation will help you understand the nature of a fraction. By understanding the values of the numerator and denominator, you will be able to determine what type of value or output the related fraction will give.
You will be able to identify if the fraction’s output is less than 1, greater than 1, or equal to 1 from the value of the numerator and denominator.
As we use fractions in our daily lives, it is important to understand the nature and relations of a numerator and denominator.
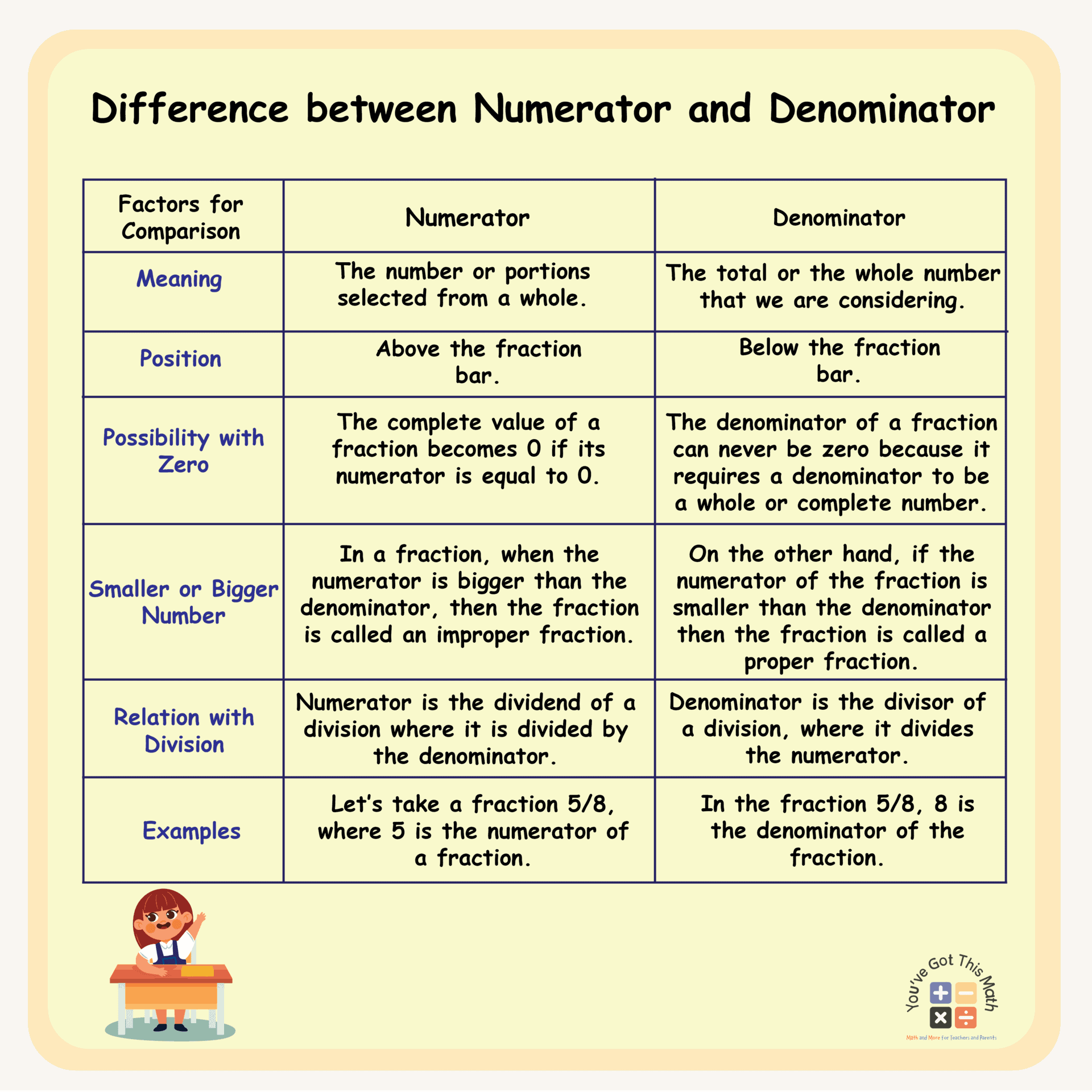
Difference between Numerator and Denominator
As we learned about the numerator and the denominator in the previous section, we got to know some facts related to them. From those facts, we are going to see what the differences are between a numerator and a denominator. See the following table for more insight.
5 Suitable Explanations to Understand What is Numerator and Denominator with Example
In the following section, you will find three fun activities regarding the numerator and denominator in the division. We mainly use these two terms in fractions. While the upper part of a fraction is called a numerator and the lower part is called a denominator.
In the first two activities, we will mainly deal with examples related to proper fractions, where the numerator is smaller than the denominator. As for the third activity, the examples are related to improper fractions. Read the details under each activity and become an expert in solving various problems of numerator and denominator.
Fractions with Smaller Numerators and Bigger Denominators
From the previous discussion, we know what a proper fraction is. Considering a fraction, x/y, when x<y, meaning when the numerator is smaller than the denominator, then it is called a proper fraction.
In a proper fraction, as the denominator is always bigger than the numerator, the quotient of a proper fraction will always be less than 1. To discuss proper fractions, we need to know about two things- unit fractions and non-unit fractions.
Explaining Unit Fraction with 1 as A Numerator.
The first question in your mind is now, what is a unit fraction? A unit fraction is a type of proper fraction, where the numerator will always be 1.
That means, from a whole or total, a unit fraction is just a singular shaded region. For example, 1/2, 1/3, 1/8, etc. are all unit fractions, as the numerators here are all 1.
To have a better understanding, see the following image. Here, you can see that every shape is divided into various regions, and only one singular region is shaded.
Explaining Non-unit Fraction Where Other Numbers than 1 are Numerator
On the other hand, a non-unit fraction is a fraction where the numerator is anything other than 1. For example, the fraction 3/8 is a non-unit fraction, where the numerator is 3. A non-unit fraction can either be a proper fraction, an improper fraction, or a whole number.
Fractions with Bigger Numerators and Smaller Denominators
In the previous section, we learned about proper fractions. Now, we are going to see the opposite scenario. That means, when the numerator of a fraction is bigger than the denominator, the fraction is called an improper fraction.
As in the improper fraction, the denominator is always smaller, and an improper fraction always has a value that is bigger than 1.
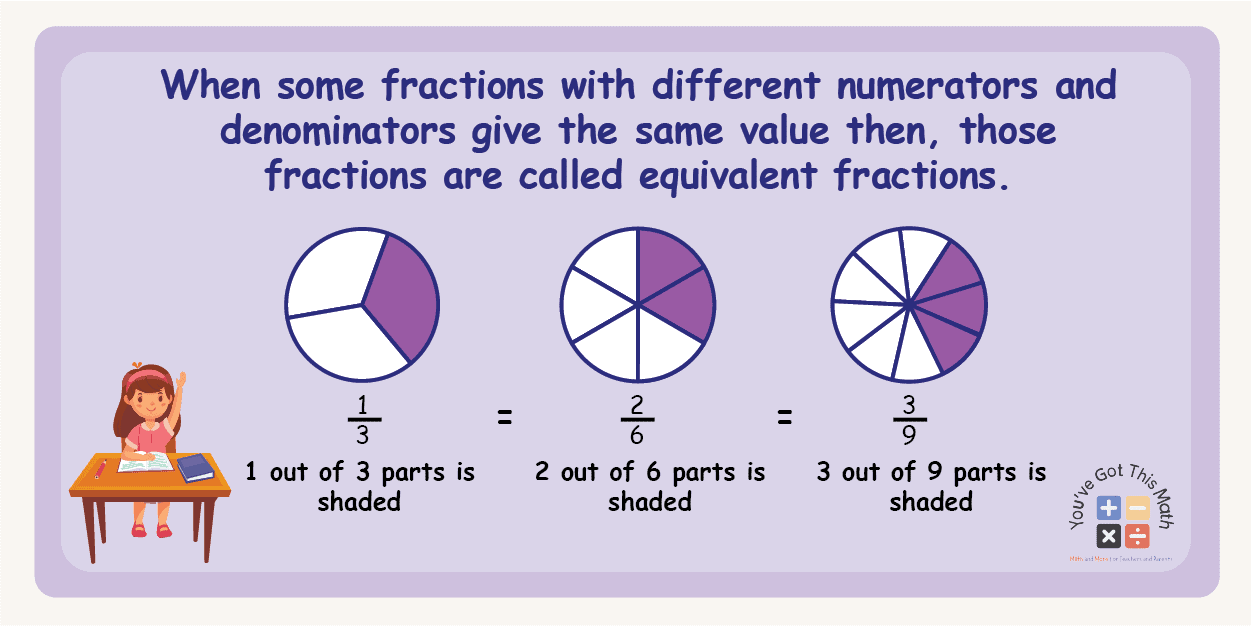
Equivalent Fraction with Different Numerator and Denominator but Represent Same Value
Now, we are going to learn about a new topic called the equivalent fraction. When some fractions with different numerators and denominators give the same value, those fractions are called equivalent fractions.
Let’s take two fractions, 1/3 and 2/6. At first glance, you will say that these two fractions aren’t equal. But look and think deeply. Take 1/3 and multiply both the numerator and the denominator by 2. This means you have to do 1×2/3×2. What do you get?
It is 2/6. Here, we have multiplied both the numerator and the denominator by a common factor, and both the fractions 1/3 and 2/6 represent the same value.
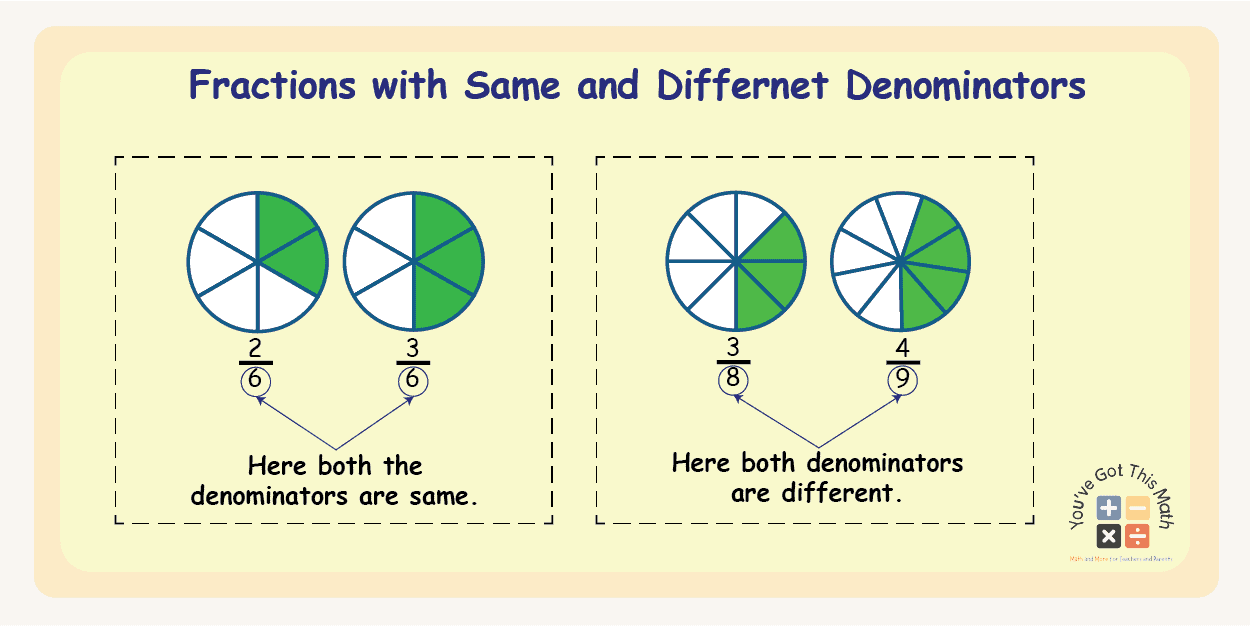
Fractions with Same or Different Denominators
Now, we are going to talk about fractions that can either have the same or different denominators. Look at the fractions 1/5, 2/5, 3/5, 7/5, etc. For the above four fractions, the denominator is always 5.
In such an instance, where the denominators of various fractions are the same, those fractions are called fractions with the same denominator.
On the other hand, look at the fractions 1/3, 2/5, 5/18, 11/25, etc., where the denominators are different for each of the fractions. These types of fractions are called fractions with different denominators.
Basic Mathematical Operations of Numerator and Denominator of a Fraction
In the following sections, we are going to see the basic operations of the numerator and denominator of fractions. These operations include addition, subtraction, multiplication, and division of numerators and denominators. Go through all the following sections for a better insight into these operations.
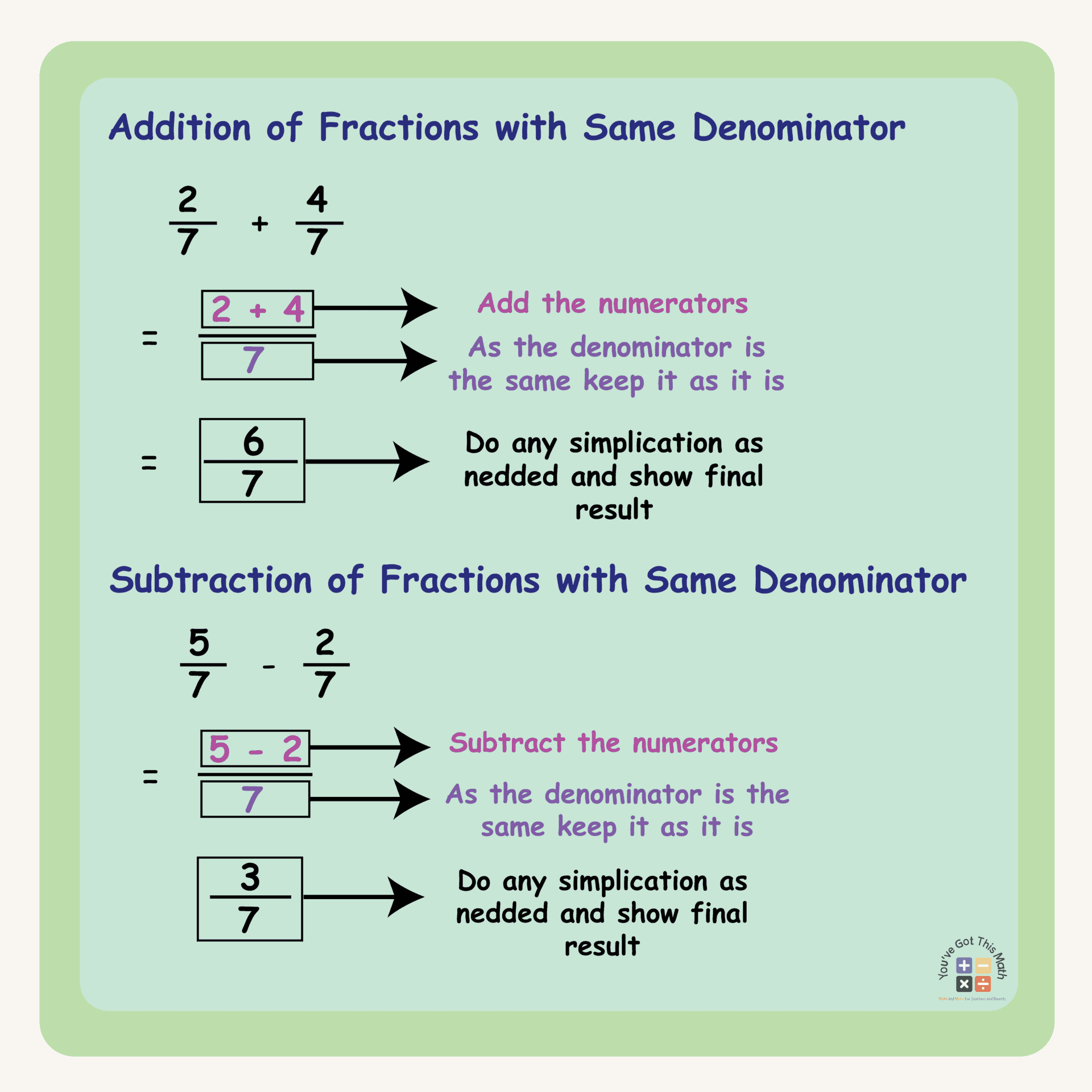
Addition and Subtraction of of Fractions with Same Denominator
This discussion will focus on adding and subtracting fractions that have the same or like denominators. The following steps will help you in this regard.
- First, note the fractions with the same denominators.
- As the denominators are the same, you don’t have to find any LCM or turn the fractions into equivalent ones.
- Just see the numerators and the operation sign, whether it is a plus or a minus.
- After that, simply add or subtract the numerator as per the question and write the answer.
- After adding or subtracting the numerators, put the denominator as it is below the numerator, and you will get the final result of that addition or subtraction operation.
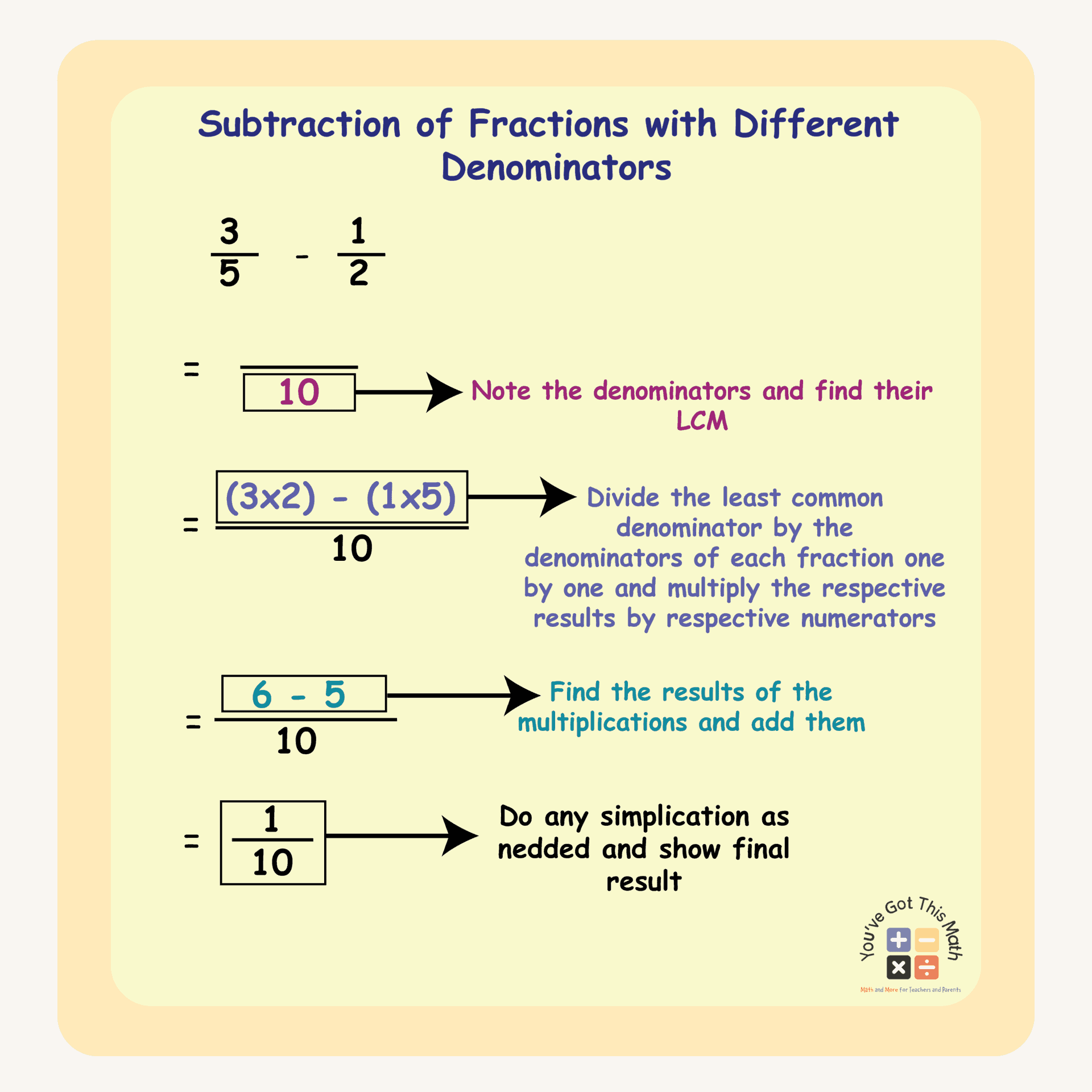
Addition and Subtraction of Fractions with Different Denominator
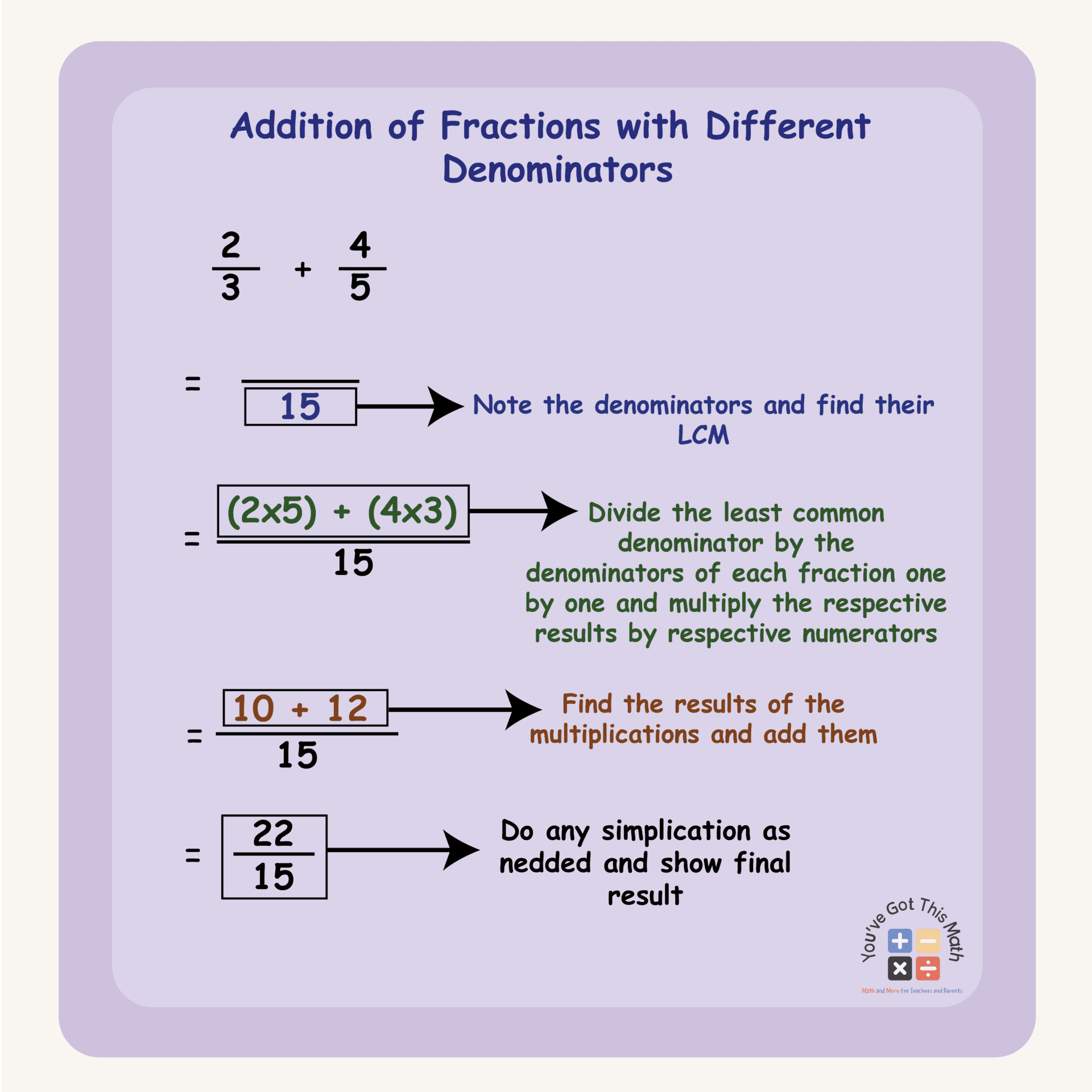
In this section, we will show you how to do the addition and subtraction of fractions with different denominators. We are going to use the LCM (least common multiple) methods for getting our problem solved. See the following steps for more details.
- Take the two fractions we need to add and identify their denominators.
- Then determine the multiples of the denominators.
- In our example, the denominators of the two fractions are 5 and 3, respectively.
- The multiples of 5 are 5, 10, 15, 25, 30, etc.
- The multiples of 3 are 3, 6, 9, 12, 15, 18, 24,
- So, we will choose 15 as the common multiple, as it is the least common among all the common multiples.
- Now, draw a line and write 15 in the lower part of the line.
- Then take the first denominator (3) and divide 15 by it. We get 5 as a result.
- Now, multiply the first numerator by 2, and we will get 10. Write 10 on the upper part of the line and add a plus sign.
- Again, divide 15 by the second denominator (5), and this time you will get 3 as a result.
- Now, multiply 3 by 4, which is the second numerator, and write 12 after the plus sign.
- Do the addition of the newly found numerators as in a previous way, and you will get 22/15 as the addition result.
- In the case of subtraction, subtract the numerators after doing all the division and multiplication instead of addition and get the subtraction result.
Add and Subtract 3 Fractions with Different Denominators
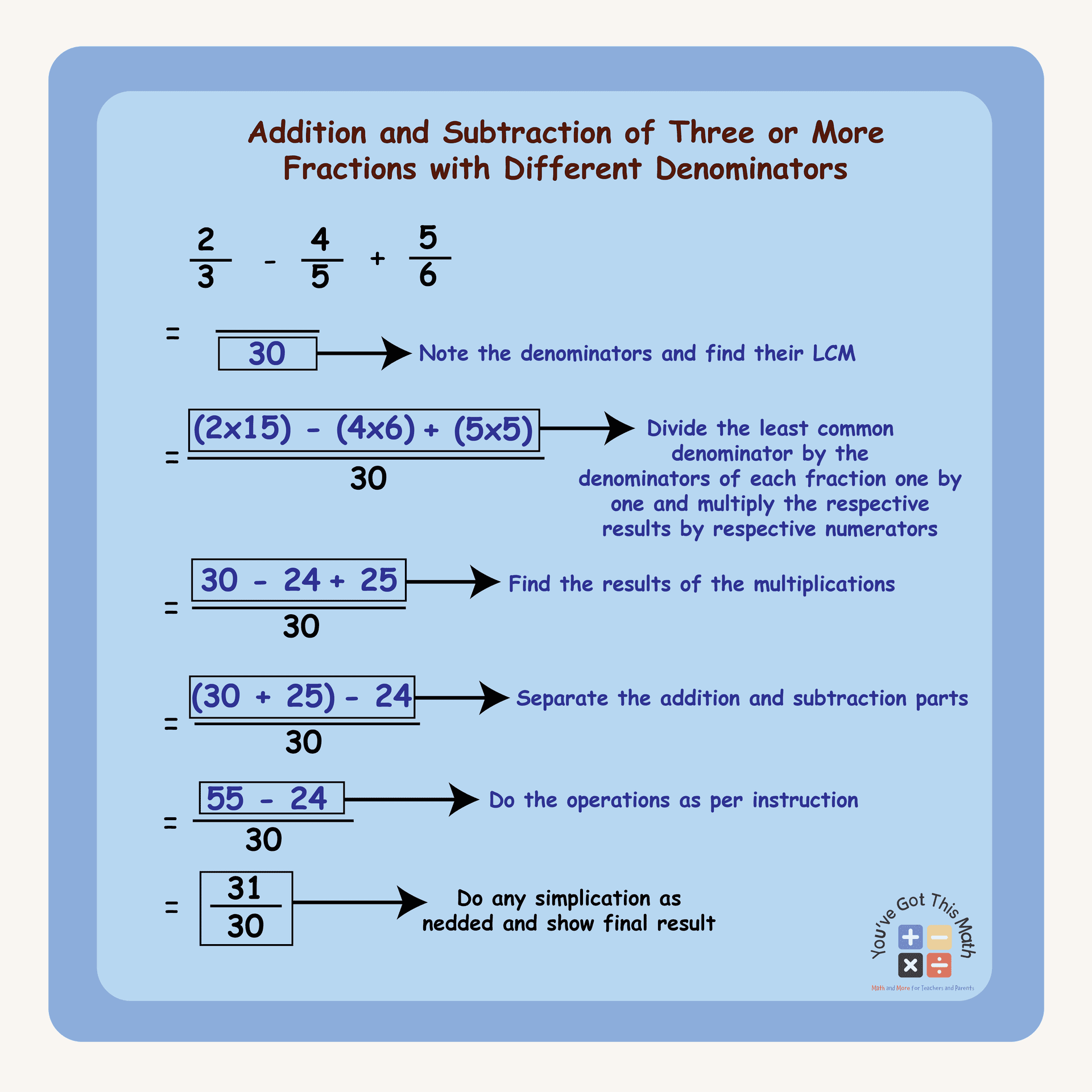
In this section, we will show you how to do the addition and subtraction of fractions in a single problem. For that, we will require more than two fractions with different denominators. See the below-given easy and simple steps below.
- Firstly, take the problem of simplification and note all the denominators.
- Then, find the LCM of the given denominators, draw a line, and write the LCM in the lower part of the line.
- Like explained in the previous example, now divide the lcm with each of the denominators of the fractions given in the problem and multiply the result with their numerators, respectively.
- Afterward, we will write the results of the multiplication one by one on the upper part of the line.
- Then, for ease of calculation, keep the addition part together inside the first bracket and the subtraction part on the other part, or vice-versa.
- Add the parts inside the bracket, then write the result. If there are two subtractions and one addition in your problem, then you have to keep the subtraction part together inside the bracket.
- Last, subtract the part from the addition result of the previous step and find the answer to this simplification.
Multiplication and Division of Numerator and Denominator of Fractions
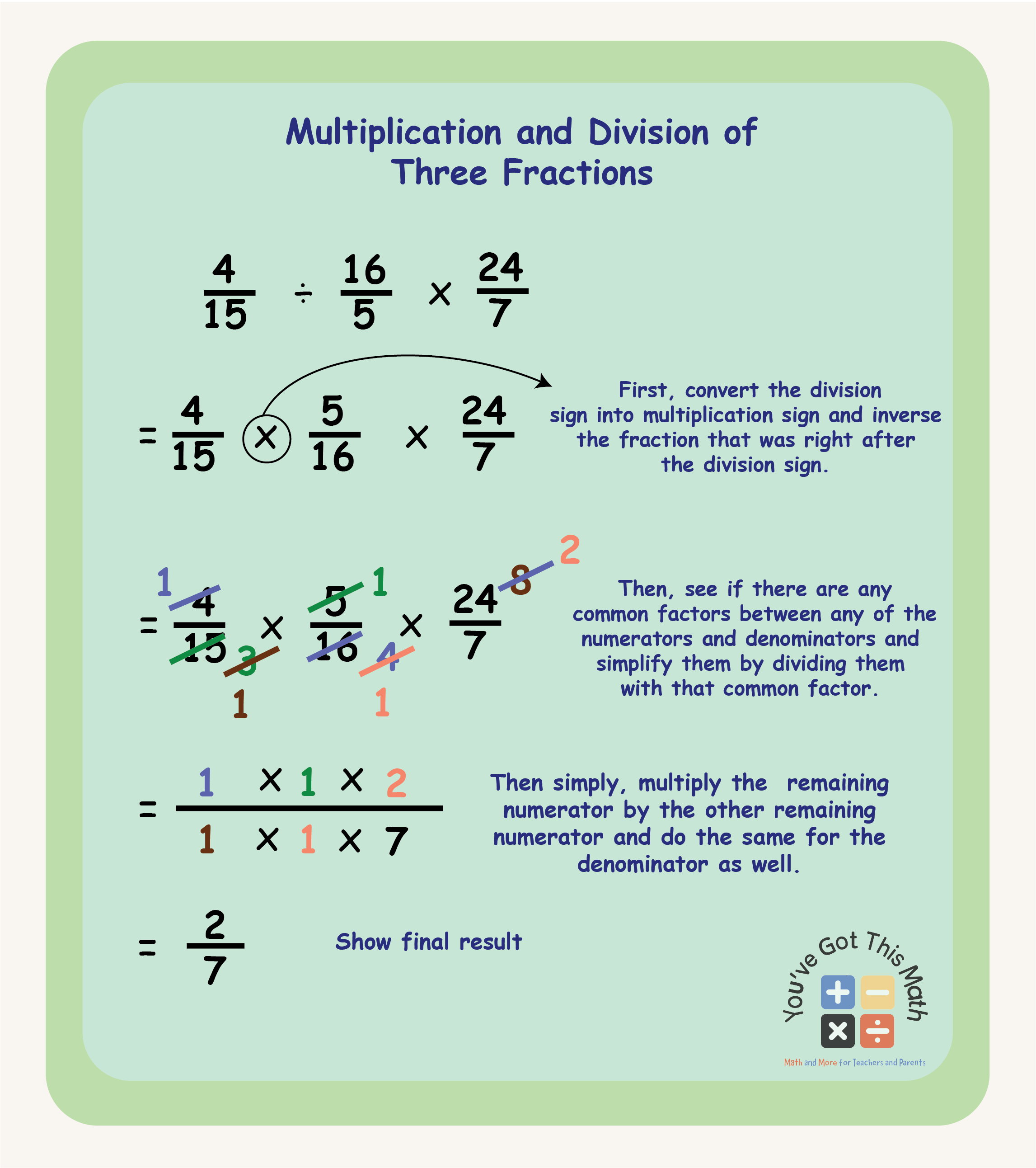
Let’s end today’s discussion, by showing you the process of multiplication and division of the numerator and denominator of fractions. The following steps will help you get better insight into these operations.
- Take the two or three fractions that you want to multiply or divide.
- If you are doing multiplication, remember that only you can divide a numerator by a denominator, or vice-versa. But you can never divide a numerator by a numerator or divide a denominator by a denominator in multiplication.
- Then see if there are any common factors between any of the numerators and denominators, and simplify them by dividing them by that common factor.
- Then simply, multiply the remaining numerator by the other remaining numerator and do the same for the denominator as well.
- After multiplication, get the final result of this operation.
- In the case of division, notice which fraction has the division sign before it.
- After marking it, convert the division sign into a multiplication sign and inverse the fraction that was right after the division sign.
- That means if the fraction was 4/5, make it 5/4 after inverting. Otherwise, you can not proceed further.
- After converting all the division signs and inverting all the required fractions, follow the same procedure as you did in the case of multiplication.
- After that, show the final result for the division.
If you have both division and multiplication in the same problem, then you have to follow the simple steps below-given steps.
- Notice and mark which fractions have division signs before them, and convert all the division signs into multiplication signs.
- After converting all the division signs, invert all the previously marked fractions that or those were/were right after the division sign.
- Then, after following the previous steps, do the same procedure as you did in the case of finding the final result of multiplication.
- After that, show the final result of the simplification.
Download Free Printable PDF
In the above discussion, I have discussed various interesting examples regarding what is numerator and denominator with example. These activities will help your students enhance their skills regarding these types of numerator and denominator identification and their operation problems.
The free what is the numerator and denominator with example PDF is available for download below. You can download this practice sheet by clicking on the download button and printing it from your device.
Please feel free to give any feedback regarding this article. Also, if your little one is having trouble doing these activities, let us know in the comment section.
Enjoy!
Hello, I am Md. Araf Bin Jayed. I have completed my B.Sc in Industrial and Production Engineering from Ahsanullah University of Science and Technology. Currently I am working as a Content Developer for You Have Got This Math at Softeko. With proper guidelines and aid from the parent organization Softeko, I want to represent typical math problems with easy solutions. With my acquired knowledge and hard work, I want to contribute to the overall growth of this organization.